Jud
- 12
- 0
I'm sure this problem is pretty trivial to most but apologies in advance, I'm just starting out sorry.
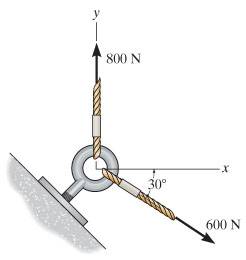
I'm not sure how to go about working this out due to the 800N
F1 (800N) x-pos = 800 tan (90)?? , y-pos = ?
F2 (600N) x-pos = 600 cos(30) , y-pos = -600 sin(30)
Homework Statement
I'm not sure how to go about working this out due to the 800N
The Attempt at a Solution
F1 (800N) x-pos = 800 tan (90)?? , y-pos = ?
F2 (600N) x-pos = 600 cos(30) , y-pos = -600 sin(30)