I Resulting force on a chamfered pneumatic piston

[inkblotch]

TL;DR Summary

What happens to the resulting force in a pneumatic cylinder, if the piston inside were chamfered.

I was reading up on forces on hydraulic/pneumatic cylinders, and I've been thinking of this for a while:

So for a pneumatic cylinder, the force on the piston is simply:
P = F/a
F = P x a
where a = area of the piston that the air pressure is acting on.

So what would happen if the piston is chamfered, thus increasing the surface area?

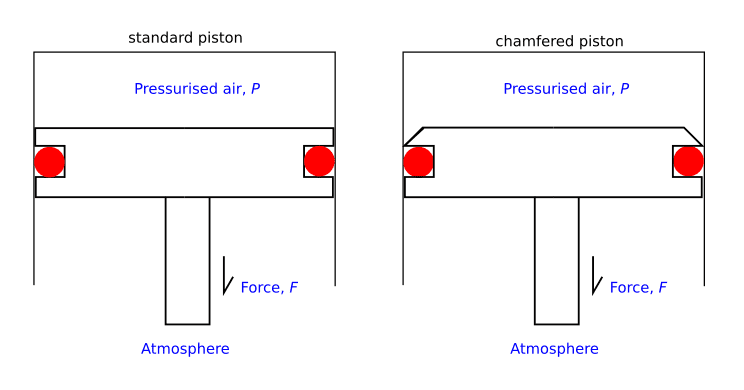
See above, (red circles are o-rings). In a closed system, my guess is :

1. The overall volume has increased, decreasing the pressure inside
2. However, surface area is increased due to the chamfer
3. Therefore the resulting downward force is the same.

Is this idea correct, or have I missed something?
Edit : The next step is, given the same air pressure, how could we estimate the increase in downward force?

 

[Chestermiller]

The pressure acts normal to the surface, so the net effect of increased surface is zero (since only the downward component of pressure matters), and the product of downward component times area is the same as total pressure times projected area.

 

[inkblotch]

So it means the chamfer can just be ignored, since the projected area of the chamfer + the area of the flat surface is the same as just the area of the completely flat piston?

 

[Chestermiller]

So it means the chamfer can just be ignored, since the projected area of the chamfer + the area of the flat surface is the same as just the area of the completely flat piston?

Yes