XYZ^2
- 2
- 0
Homework Statement
Find impedance and Io.
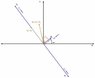
draw phasor diagram for rlc circuit
V = 120cos(2π525t) where R = 10Ω, C = 1μF, L = 100mH, Vo = 120V
Homework Equations
Z = √(R2 + (ωL-1/(ωC))^2) = √(10^2 + (2π * 525 Hz * 100 mH - 1/(2π * 525 Hz * 1 μF ))^2) = 28.525Ω
Io = Vo/Z = 120 V / 28.525 Ω = 4.207 A
tan ϕ = (ωL - 1/(ωC))/R = (2π525 * 100 mH - 1/(2π525 *1 μF)) / 10 Ω = -15882.508
ϕ = -1.5707 rad = -89.996°
VRo = IoR = 4.207 A * 10Ω = 42.07 V
VCo = Io/(ωC) = 4.207 A / (2π525 * 1 μF) = 1275.361611 V
VLo = IoωL = 4.207 A * 2π525 * 100 mH = 1387.751431 V
Vo = √(VR02 + (VLo- VCo)^2 ) = 120.0056523 V
The Attempt at a Solution
I get a negative phase angle which should mean that capacitance is greater than inductance but this is not the case based on values above.
when I draw out a rough phasor diagram I have voltage ahead of current.
not sure where i went wrong.
note: diagram attached is rough and not to perfect scale