I'll borrow your picture for a while. Thanks in advance

k4ff3 said:
Thank you for being so patient.
- In the rolling case (r): How can the gravitational PE be transformed into rotational PE?
- In the sliding case (s): How can the gravitational PE "go into whatever is applying the force f"?
- How does nature know that she should transform exactly the same amount of grav. PE to rot PE in r, as she transforms grav. PE to "the force applier" in s?
- How can an object (in rest) of the same mass as the sylinder have the same PE(=mgh) as the moving bodies (in an instant where they all are at the same height), when the moving bodies constantly are leaking Potential Energy?
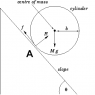
- Why is the force applied at the edge of the cylinder (i.e the friction force f) internal, but the force f applied to the COM external?
Ooh, you are going away from the right track
Let's go from the start. We have 2 cases:
CASE 1: Rolling.
In this case, let's make another assumption: the cylinder rolls without slipping, i.e. \vec{v_A}=0. This will make things easier and concurs with what Doc Al said. Because of that assumption, friction in this case doesn't do any work on the cylinder (it's static friction!). Let's assume that the cylinder starts moving from rest.
By the energy conservation law:
PE = KE = translational KE + rotational KE
This concurs with the statement of Doc Al, "
some of that PE is transformed into
rotational KE". In addition, friction doesn't do work, but the cylinder gains both translational and rotational KE, not translational KE only as in the "sliding" case. This is why people usually say, static friction in this case only does the job of transferring a part of PE into rotational KE.
CASE 2: Sliding.
Because now the force f is applied at the center, whose velocity is not zero, f does do work on the cylinder. Besides, we have already known that the cylinder does not rotate in this case.
Therefore:
PE - (work of f) = KE = translational KE
In addition, we all agree that the translational motions in 2 cases are the same, so translational KE in case 1 = translational KE in case 2. Now do you agree with me that total KE in case 2 (sliding) is smaller than in case 1 (rolling)?
For the above questions of yours:
_ #1 and 2: Maybe you mean "rotational KE" instead of "rotational PE"?
In general, PE will transfer into any other kind of energy if the object decreases its height. The object, initially, already has an amount of PE, i.e. it has the potential to gain kinetic energy or any other kind of energy if it goes down. This is because of the law of energy conservation.
_ #3: Nature only knows static friction doesn't do any work (i.e. \vec{v}_A=0, and that's the only thing she wants. It's like an initial condition. If it's not static friction, things will change. And because it's static friction, friction doesn't do work, which leads to so many results afterward.
So why static friction? It's the nature of the interaction between the material of the ground and the material of the cylinder, and I have no answer for that.
_ #4: Now it's like you have $100. Staying at rest = no trading, the money remains the same. If you trade $100 for shares, you will have, say, 100 shares.
But if you are investing in something, buying shares for example, your money will go down as you have more shares (or more KE!). Maybe yesterday you had $101, and tomorrow you will have $99, but now, you still have $100, and you have the potential to have 100 shares if you use up your money. The same thing goes for PE. People don't call it "POTENTIAL energy" for nothing!
_ #5: If we consider the cylinder only, friction and the "f" force are never internal forces. Friction is the force by the ground, so it is external force.