lightlightsup
- 100
- 11
Therefore, if someone were to ask what the magnitude of centripetal acceleration is at the top of the wheel at a given instant (relative to the ground):
##v_{cm} = v_{translational, center-of-mass/wheel}##
##ω = ω_{point-of-contact}##
##v_{top} = 2(v_{cm}) = 2(rω)##
##a_{c(top)} = \frac{v_{top}^2}{R} = \frac{(2v_{cm})^2}{2r} = \frac{2(v_{cm})^2}{r} = \frac{2(ωr)^2}{r} = 2ω^2r##
I think this is correct.
But, what is the ##ω## and ##α## about the center of the wheel?
Also, what is the ##a_{c(top)}## relative to the center of wheel? Would that even make sense?See this image:
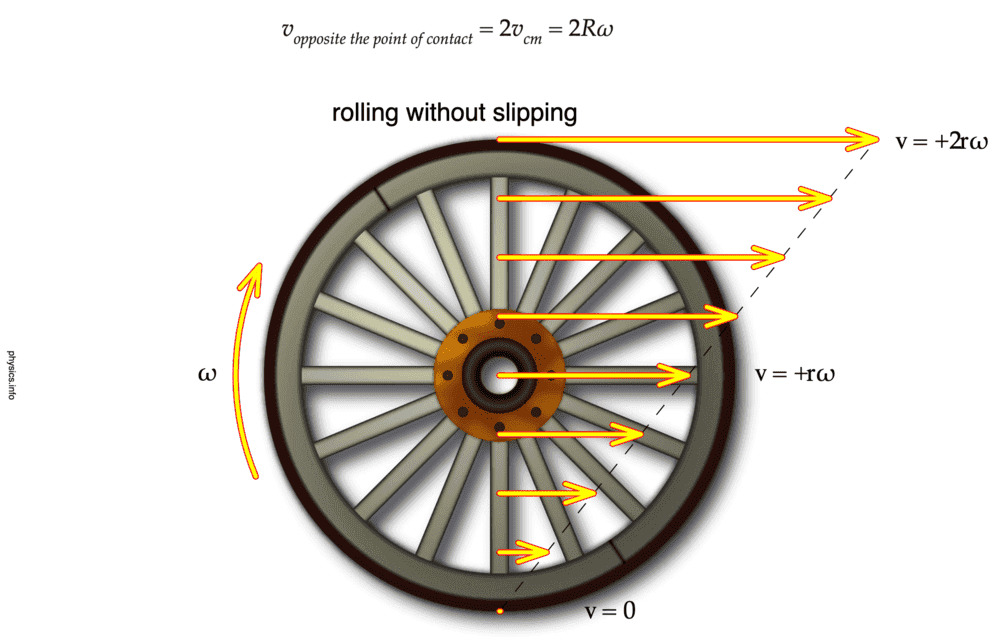
##v_{cm} = v_{translational, center-of-mass/wheel}##
##ω = ω_{point-of-contact}##
##v_{top} = 2(v_{cm}) = 2(rω)##
##a_{c(top)} = \frac{v_{top}^2}{R} = \frac{(2v_{cm})^2}{2r} = \frac{2(v_{cm})^2}{r} = \frac{2(ωr)^2}{r} = 2ω^2r##
I think this is correct.
But, what is the ##ω## and ##α## about the center of the wheel?
Also, what is the ##a_{c(top)}## relative to the center of wheel? Would that even make sense?See this image:
Last edited: