FFX
- 8
- 0
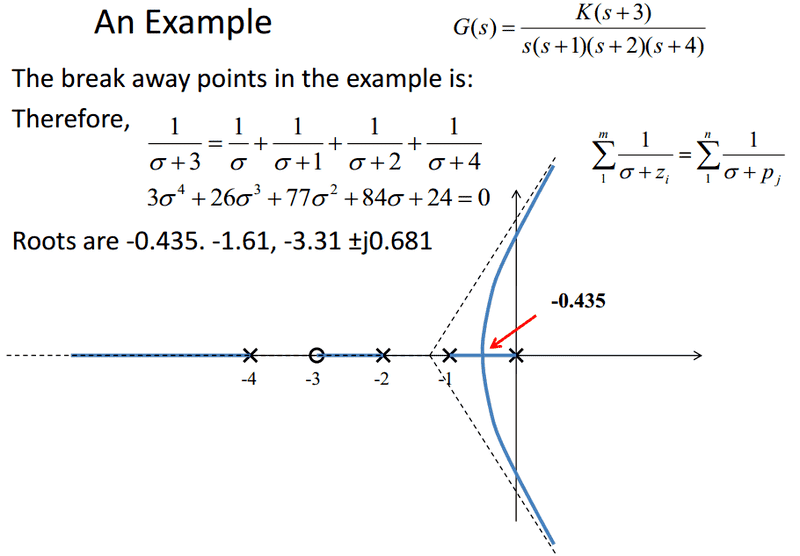
Hi guys. Firstly the answer to the requirement of the post is all in the picture (problem statement, relevant equations etc.). I'm just wondering if someone could tell me why they use the root -0.435 as the breakaway point? Like I know there's two real roots; -0.435 and -1.61, so obviously one of those two are the breakaway. Is it simply -0.435 because the rule is that two poles can never intersect? Or is it for an additional reason? Like I could apply the two poles never intersection rule to this scenario, but I'm wondering if there's another reason. Such as what were to happen if the roots were -0.435 and -0.675, or is such a thing not possible?