Roots of a polynomial and differenciaton

  • Thread starter Thread starter babita
  • Start date Start date
  • Tags Tags
    Polynomial Roots
Click For Summary

Homework Help Overview

The discussion revolves around the relationship between the roots of a polynomial and its derivative, specifically focusing on the implications of a derivative being zero within a given interval. Participants are exploring the conditions under which a polynomial may have real or complex roots.

Discussion Character

  • Exploratory, Conceptual clarification, Assumption checking

Approaches and Questions Raised

  • Participants question why a polynomial might have a maximum of two real roots instead of exactly two, considering cases of repeated roots. There is discussion about the nature of roots in relation to the discriminant and the behavior of the derivative.

Discussion Status

The conversation is active, with participants sharing examples and attempting to clarify concepts related to real and complex roots. Some have provided specific polynomial examples to illustrate their points, while others are reflecting on the implications of the derivative's behavior.

Contextual Notes

Participants mention the discriminant and its role in determining the nature of roots, noting cases where the discriminant is less than zero, which leads to complex roots. There are also references to specific polynomial equations and their derivatives.

babita
Messages
61
Reaction score
0

Homework Statement


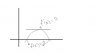
I read that if f'(x) is zero once in [a b] then f(x) has maximum two real roots.
Why maximum? Shouldn't it be exactly 2?
Or it has something to do with the case of repeated roots?

Homework Equations





The Attempt at a Solution


was thinking as in figure
 

Attachments

  • Untitled.png
    Untitled.png
    4.6 KB · Views: 472
Physics news on Phys.org
Well in your case it has exactly two real roots, but in another case you might only have one real root or none. Try it out and draw a graph and see what you get. Often there would be one real root and one imaginary root.
 
oh...like a quadritic equation with D=o , will have f'(x)=0 at -b/2a but it does not have any real roots ?
 
Thanks :)
 
Ok take for example x^2+x+1. Does this have any real roots? If yes then what are they?
 
no it doesn't have any real roots. but f'(x)=0 at x=-0.5
right?
 
sry typing mistake i there meant D<0
 
Yes you are correct. You take it's derivative, and you have to see where that derivative equals 0. Like in the equation i gave you 2x+1=0 implies that 2x+1=0 if and only if x=-0.5.
 
babita said:
sry typing mistake i there meant D<0


Yes if you have the a negative discriminant, then you have two complex roots which are complex conjugates of one another.
 

Similar threads

Why are there only two roots of this cubic polynomial?
  • · Replies 6 ·
Replies
6
Views
2K
Roots of a polynomial mixed with a trigonometric function
  • · Replies 14 ·
Replies
14
Views
2K
Undergrad Quintic Polynomial Tschirnhaus Transform: Possible complex Bring Radicals
  • · Replies 0 ·
Replies
0
Views
3K
Solve the problem involving the cubic function
  • · Replies 12 ·
Replies
12
Views
2K
Find the value of ##a, b## and ##k## in the problem involving graphs
  • · Replies 6 ·
Replies
6
Views
2K
How do you divide polynomials in your head "on sight"?
  • · Replies 27 ·
Replies
27
Views
5K
Quadratic equation with roots of opposite signs
  • · Replies 6 ·
Replies
6
Views
3K
Using binomial coefficients to find sum of roots
  • · Replies 3 ·
Replies
3
Views
2K
Solving a 3rd Degree Polynomial: What are the Options?
  • · Replies 10 ·
Replies
10
Views
3K
Both roots of a quadratic equation lying within limits
  • · Replies 22 ·
Replies
22
Views
3K