- #1
kalisky
- 4
- 0
Hi,
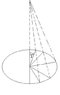
Let's say I have a flat circle on the x-y axes, and I am looking at it from along the z-axis.
now let's say I rotate it along the x-axis by A(alpha) degrees, and take a 2D picture, I would receive an ellipse, right?
now let's say I would like to have a function from an angle T(theta), which gives me a point on the original flat circle, to an angle G(gama), which gives me a point on the projected ellipse.
Anyone?
Let's say I have a flat circle on the x-y axes, and I am looking at it from along the z-axis.
now let's say I rotate it along the x-axis by A(alpha) degrees, and take a 2D picture, I would receive an ellipse, right?
now let's say I would like to have a function from an angle T(theta), which gives me a point on the original flat circle, to an angle G(gama), which gives me a point on the projected ellipse.
Anyone?