lavankohsa
- 32
- 0
Homework Statement
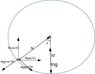
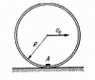
A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane; at the moments when the body A gets into the lower position, the center of the hoop moves with velocity v0. At what values of v0 will the hoop move without bouncing?
Homework Equations
mgcos(θ)−N=mv2/R
One equation will be the energy equation. The velocity of hoop and mass A will reduce as the body A is gaining the potential energy.