Rotation Problem, I'm confused on this one

  • Thread starter Thread starter PremedBeauty
  • Start date Start date
  • Tags Tags
    Confused Rotation
Click For Summary

Homework Help Overview

The problem involves a rod with particles attached, rotating around a perpendicular axis. The task is to determine the work required to change the rotational rate at specified intervals and to analyze the relationship between kinetic energy and rotational rate.

Discussion Character

  • Exploratory, Assumption checking

Approaches and Questions Raised

  • Participants discuss the rotation of the mass and question whether it is rotating about point O or the rod itself. There is confusion regarding the moment of inertia and the missing radius of the rod. One participant suggests using the work-energy theorem.

Discussion Status

The discussion is ongoing, with participants seeking clarification on the setup and parameters of the problem. Some guidance has been offered regarding the work-energy theorem, but no consensus has been reached on the interpretation of the problem.

Contextual Notes

There are constraints related to missing information, such as the radius of the rod and the total mass of the system. The urgency of the homework deadline is also noted by the original poster.

PremedBeauty
Messages
25
Reaction score
0
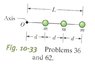
.0100kg particles have been glued to a rod of Length L=6.00cm and negligible mass and can rotate around a perpendicular axis through point O at one end. How much work is required to change the rotational rate (a) from 0-20.0 rad/s, (b) from 20.0 rad/s to 40.0 rad/s, and (c) from 40.0 rad/s to 60 rad/s? (d) what is the slope of a plot of the assembly's kinetic energy in joules versus the square of its rotational rate (in radians-squared per second squared)?

----->The question in my mind is the rotation. Is the mass rotating about O? Or is it rotating around the rod? You have to figure the moment of inertia. The radius of the rod is not given, if the rod is rotating on its axis. And, the total mass is not given "0.0100kg particles" is all that is mentioned. I've been working on this problem for hours and don't understand how to finish it and it
s due tomorrow and I have so much left to do in my other classes:cry:
 

Attachments

  • physicspic.jpg
    physicspic.jpg
    14.5 KB · Views: 628
Physics news on Phys.org
Cannot yet see your diagram so I do not know where the masses are or how many. The problem says it is rotating about a perpendicular axis- that means perpendicular to the length of the rod.
 
The diagram is on now, it just takes alittle while to load.
 
PremedBeauty said:
The diagram is on now, it just takes alittle while to load.

Unfortunately it is not on.
 
Set up the work-energy theorem!
 

Similar threads

Undergrad What Happens to Rotational Velocity When AC Part is Dropped?
  • · Replies 4 ·
Replies
4
Views
1K
Spin-1 particle states as seen by different observers: Wigner rotation
  • · Replies 5 ·
Replies
5
Views
3K
Uniform rotating rod about a point at one end of the rod
  • · Replies 3 ·
Replies
3
Views
3K
How Do You Calculate Angular Acceleration in a Pivoting Rod Problem?
  • · Replies 1 ·
Replies
1
Views
2K
Rotating rod of negligible mass attached to two point masses
  • · Replies 19 ·
Replies
19
Views
4K
Undergrad Rotating plate thrown parallel to ground
  • · Replies 2 ·
Replies
2
Views
1K
Undergrad Confused about the axis of rotation in rotational motion w/o slipping
  • · Replies 10 ·
Replies
10
Views
4K
How Does Torque Affect the Motion of a Disc Pulled Across a Table?
  • · Replies 3 ·
Replies
3
Views
2K
Rotational momentum (previous problem)
  • · Replies 6 ·
Replies
6
Views
7K
Precession of Rotating Rigid Body from Two Different Frames
  • · Replies 2 ·
Replies
2
Views
2K