Rotational Dynamics Problem - Rod slipping against Block

[Tanya Sharma]

Homework Statement

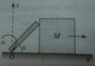
A uniform rod of mass m and length l is pivoted at point O. The rod is initially in vertical position and touching a block of mass M which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point O. This causes the block to move forward. The rod loses contact with the block at θ = 30°. All surfaces are smooth.

1. The value of M/m?
2. The velocity of block when the rod loses contact with the block?
3. The acceleration of center of mass of rod, when it loses contact with the block?
4. The hinge reaction at O on the rod when it loses contact with the block?


Ans 1) 4:3
2)√(3gl)/4
3) (3g)/4
4)(mg/4)j

Homework Equations

The Attempt at a Solution

The speed of the tip of the rod in horizontal direction is same as that of the block .

Let V be the speed of the block when rod loses contact with block.
So,Horizontal speed of the tip of the rod = V
Component of speed perpendicular to length of the rod =$V_{\bot}$ = VSin30°=V/2
Angular speed of the rod at the instant block leaves contact with the rod =$\frac{V_{\bot}}{l}$ = $\frac{V}{2l}$

Applying Conservation of Energy ,

Loss in Potential Energy of Rod = Gain in Rotational Kinetic Energy of Rod + Gain in KE of Block

$\frac{Mgl}{2}(1-Sin60°) = \frac{1}{2}\frac{ml^2}{3}(ω ^2) +\frac{1}{2}MV^2$

$\frac{Mgl}{2}(1-Sin60°) = \frac{1}{2}\frac{ml^2}{3}\frac{V ^2}{4l^2} +\frac{1}{2}MV^2$

$\frac{Mgl}{4} = \frac{mV^2}{24} +\frac{1}{2}MV^2$

Is my approach correct ? Now ,how am I supposed to proceed further ? one more equation is required to solve the problem ...

 

[haruspex]

So,Horizontal speed of the tip of the rod = V
Component of speed perpendicular to length of the rod =$V_{\bot}$ = VSin30°=V/2

No, that's backwards. Which way is the tip of the rod moving?

$\frac{Mgl}{2}(1-Sin60°) = \frac{1}{2}\frac{ml^2}{3}(ω ^2) +\frac{1}{2}MV^2$

Not sin(60), I think. But I see that you actually used the right value below.

how am I supposed to proceed further ?

Maybe energy alone won't cut it, and you need to use forces and accelerations. This could be because the energy equation fails to capture the fact that the tip of the rod and the block have moved the same horizontal distance in the same time.

 

[Tanya Sharma]

Thank you very much for the reply...I understand my mistake...

The component of angular speed of the tip of the rod in horizontal direction is same as that of the block .

Let V be the speed of the block when rod loses contact with block.
So,Horizontal component of angular speed of the tip of the rod = ωlcos60°=V

So,ωl/2=V
Thus,ω = 2V/l

Applying Conservation of Energy ,

Loss in Potential Energy of Rod = Gain in Rotational Kinetic Energy of Rod + Gain in KE of Block

$\frac{Mgl}{2}(1-Sin60°) = \frac{1}{2}\frac{ml^2}{3}(ω ^2) +\frac{1}{2}MV^2$

$\frac{Mgl}{2}(1-Sin60°) = \frac{1}{2}\frac{ml^2}{3}\frac{4V ^2}{l^2} +\frac{1}{2}MV^2$

$\frac{Mgl}{4} = \frac{2mV^2}{3} +\frac{1}{2}MV^2$

Maybe energy alone won't cut it, and you need to use forces and accelerations. This could be because the energy equation fails to capture the fact that the tip of the rod and the block have moved the same horizontal distance in the same time.

I have thought in terms of forces...but really haven't been able to relate things...

The forces on the rod are

Hinge force in x direction = H_x
Hinge force in y direction = H_y
Force due to gravity = mg
Normal contact force from the block = N

The force on the block are

Normal contact force from the rod = N

I know how to calculate acceleration and torques but i am unable to relate them so that given condition in the question is satisfied.

Please can you explain ?

 

[haruspex]

I have thought in terms of forces...but really haven't been able to relate things...

Don't worry about the force at the hinge. The critical statement we have to turn into an equation is that the normal force vanishes. In terms of the angular speed and acceleration, what is the acceleration of the block (be very careful with that one), the normal force on the block, and the torque on the rod?

 

[Tanya Sharma]

Net torque on the rod about pivot =$mg\frac{l}{2}cosθ -Nlsinθ$
where θ is the angle which rod makes with the horizontal

The acceleration of the block is a=N/M where N is the normal contact force between block and the rod

Since ,ωl/2=V

Therefore , differentiating above we get,
αl/2=a

 

[haruspex]

Right, so relate that to the angular acceleration of the rod, relate N to the linear acceleration of the block, and relate that acceleration back to the angular acceleration and velocity of the rod.

 

[Tanya Sharma]

Oh...sorry I have edited my earlier post...

The acceleration of the block is a=N/M where N is the normal contact force between block and the rod

Since ,ωl/2=V

Therefore , differentiating above we get,
αl/2=a

 

[haruspex]

Oh...sorry I have edited my earlier post...

The acceleration of the block is a=N/M where N is the normal contact force between block and the rod

Since ,ωl/2=V

Therefore , differentiating above we get,
αl/2=a

No, please work with the forces. Your method above merely expresses the assumption that the two stay in contact. To find when they, in fact, would not we need to look at forces. (You will need the polar coordinate formula for acceleration of the tip.)

 

[Tanya Sharma]

I don't know how to work with polar coordinates...I would be grateful if you could tell me the polar coordinate formula for acceleration of the tip.

 

[haruspex]

I don't know how to work with polar coordinates...I would be grateful if you could tell me the polar coordinate formula for acceleration of the tip.

I expect you do, but maybe not with that terminology. If the rod were rotating at constant angular speed it would nonetheless have an acceleration, right? What's the formula for that and in which direction does it operate? Since the angular speed is not constant it has another linear acceleration. What's the formula and direction of that?

 

[ehild]

I don't know how to work with polar coordinates...I would be grateful if you could tell me the polar coordinate formula for acceleration of the tip.

You know that the coordinates of the tip of rod are y=Lsin(θ) and x=Lcos(θ)
You can find the components of acceleration in terms of derivatives of θ. The tip of the rod is at the same x coordinate as the left side of the block, so the second derivative of x is the acceleration of the block. What force acts on the block? What is the force when the rod loses contact with the block?

ehild

 

[Tanya Sharma]

ehild...Thank you

You know that the coordinates of the tip of rod are y=Lsin(θ) and x=Lcos(θ)
You can find the components of acceleration in terms of derivatives of θ. The tip of the rod is at the same x coordinate as the left side of the block, so the second derivative of x is the acceleration of the block.
ehild

$\frac {d^2x} {dt^2} = -Lcosθ$

What does -ve sign signify??

What force acts on the block?

Force on the block = N
Thus, N=-MLcosθ . I am not sure about the -ve sign.

What is the force when the rod loses contact with the block?

There is no force horizontally on the block when it loses contact with the rod i.e N=0

 

[ehild]

ehild...Thank you
$\frac {d^2x} {dt^2} = -Lcosθ$

Try again.

x=Lcos(θ), but θdepends on t.

dx/dt = -Lsin(θ)(dθ/dt)

d²x/dt²=...?ehild

 

[Tanya Sharma]

Do we have to take θ = ω₀t + (1/2)αt² where ω₀ =0 ?

 

[ehild]

Do we have to take θ = ω₀t + (1/2)αt² where ω₀ =0 ?

NO, why do you think that the angular acceleration is constant? θ is a function of t, ω is its first derivative and α is the second derivative with respect to t.

ehild

 

[Tanya Sharma]

x=Lcos(θ)

dx/dt = -ωLsin(θ)

d²x/dt²= -L(ωcosθ + αsinθ)

 

[ehild]

You know product rule and chain rule of differentiation? x is function of θ but θ is function of t. The velocity is function of θ and ω, both depend on t.
ωsin(θ) is a product of two functions.
Apart from Physics, how do you calculate the first and second derivative of a function f(g(t))?

ehild.

 

[Tanya Sharma]

You know product rule and chain rule of differentiation? x is function of θ but θ is function of t. The velocity is function of θ and ω, both depend on t.
ωsin(θ) is a product of two functions.
Apart from Physics, how do you calculate the first and second derivative of a function f(g(t))?

ehild.

x=Lcos(θ)

dx/dt = -Lsin(θ)(dθ/dt)

d²x/dt²= -L [cosθ(dθ/dt) + sinθ(d²θ/dt) ]

 

[ehild]

Not quite... d²x/dt²= -L [cosθ(dθ/dt)² + sinθ(d²θ/dt²) ]= -L(cosθ ω²+sinθ α).

What force acts on the block?

What is the acceleration of the block when it loses contact with the rod?

How are ω and α related at that moment?

ehild

 

[Tanya Sharma]

d²x/dt²= -L [cosθ(dθ/dt)² + sinθ(d²θ/dt²) ]

The first term in the bracket on the right side should be cosθ(dθ/dt) .Here we keep dθ/dt constant and differentiate sinθ .

 

[ehild]

The first term in the bracket on the right side should be cosθ(dθ/dt) .Here we keep dθ/dt constant and differentiate sinθ .

You have to differentiate sinθ(t). d(sinθ(t))/dt=cosθ(dθ/dt). And it was multiplied with dθ/dt. So the first term is cosθ (dθ/dt)².

ehild

 

[Tanya Sharma]

ehild...You are right

So now we have acceleration of the tip of the rod as

d²x/dt²= -L [cosθ(dθ/dt)² + sinθ(d²θ/dt²) ]= -L(cosθ ω²+sinθ α).

Force acting on the block = N

Accelaration of the block =N/M

So, N/M = -L(cosθ ω²+sinθ α).

Is that so??

 

[ehild]

Yes, you can also write that N= -LM(cosθ ω²+sinθ α).And what is N at the moment when the rod and block lose contact?

ehild

 

[Tanya Sharma]

N=0 at this moment.Putting N=0 ,we get

ω² =-αtanθ

now Iα = mg(l/2)cosθ at the moment rod loses contact .

I get correct values for first three parts .

Now, how to deal with last part where we have to calculate hinge force ??

 

[ehild]

You work very fast.
The force at the hinge can be determined if you know the acceleration of the centre of mass, which is the sum of all forces divided by m.

What is the acceleration of the COM at angle θ =30°?

ehild

 

[Tanya Sharma]

a_com=3g/4.I have calculated it from the radial and tangential components.

Is there another way of calculating it??

 

[ehild]

What is the direction of a_com?
You can get the components of the acceleration of COM also from the acceleration of the tip.
a_comx=0.5d²x/dt², a_comy=0.5d²y/dt²

ehild

 

[Tanya Sharma]

How are both the x and y components half of the acceleration of the tip of the rod?? I mean , I don't understand how the accelerations of COM and the tip are related ??

 

[ehild]

How are the coordinates of the COM related to those of the end of rod, supposed that the origin is at the hinge?

ehild

 

[Tanya Sharma]

Okay...i understand what you say...

Why is there a -ve sign in the expression for N and ω² ? I mean what does the -ve sign signify considering ω² is a positive quantity.