Metalsonic75
- 28
- 0
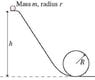
The marble rolls down a track and around a loop-the-loop of radius R. The marble has mass m and radius r (see picture). What minimum height h must the track have for the marble to make it around the loop-the-loop without falling off?
This is driving me nuts. I know that the total mechanical energy at the top of the track (starting point) is mgh, and at the top of the loop, it is mgR + 1/2mv^2 + 1/2I\omega, so mgh = mgR + 1/2mv^2 + 1/2I\omega. I then substituted 2/5mr^2 for I (general I of a sphere), and v/r for \omega. Leaving that for a moment, I found that the sum of forces at the top of the loop are F = ma_c = m*(v^2/r) = mg - n. Since I'm trying to find the point where n=0, I substituted 0 for n, and solved for g = v^2/r. Then I substituted v^2/r for g in my earlier equation that I obtained for total mechanical energy. Simplifying everything gave me h = R + 0.7r, which is incorrect. I would really like to know where my error lies. The answer must include the variables r and R. Any help would be appreciated. Thank you.
This is driving me nuts. I know that the total mechanical energy at the top of the track (starting point) is mgh, and at the top of the loop, it is mgR + 1/2mv^2 + 1/2I\omega, so mgh = mgR + 1/2mv^2 + 1/2I\omega. I then substituted 2/5mr^2 for I (general I of a sphere), and v/r for \omega. Leaving that for a moment, I found that the sum of forces at the top of the loop are F = ma_c = m*(v^2/r) = mg - n. Since I'm trying to find the point where n=0, I substituted 0 for n, and solved for g = v^2/r. Then I substituted v^2/r for g in my earlier equation that I obtained for total mechanical energy. Simplifying everything gave me h = R + 0.7r, which is incorrect. I would really like to know where my error lies. The answer must include the variables r and R. Any help would be appreciated. Thank you.