Rotational Mechanics Homework: Equations & Solution for Part 1 Work

[PhysicsFuture]

Homework Statement

Homework Equations

E=T+U
T=1/2 mv^2
U=∫F⋅dr

The Attempt at a Solution

Part 1 Work
x=x-dot
y=y-dot
z= z-dot
r=r-dot
θ=θ-dot
[/B]
T= 0.5m(x^2 +y^2) 0.5M(z)^2
Changing to polar coordinates
T=0.5m(r^2 +rθ^2) 0.5M(z)^2

U=-Mgz

E=T+U
=0.5m(r^2 +rθ^2) 0.5M(z)^2-Mgz

z=L-r

= 0.5m(r^2 +rθ^2) 0.5M(z)^2-Mg(l-r)


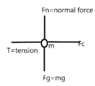
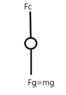
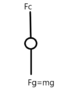
I drew the FBD for both:
for mass on table

Fx
Fc-T=ma

Fc= mrw^2
T=Mg
mrw^2-Mg=ma

a=rw^2-(Mg)/m
v=rw^2-(Mg)r/m

for hanging mass

Fc-Fg=0
Fc=Fg
Fc=Mg

No accleration or velocity

Is this the right track

 

[kuruman]

Please label your solution(s) with the number(s) of the part(s) that you are solving,