CptCavin
- 2
- 0
- TL;DR Summary
- Tipping Moment and Righting Moment of an object on a rubber platform.
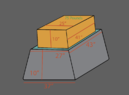
I am trying to understand how to find the righting moment of an inflatable trapezoid with 75-pounds at the top. The object at the top is 10" tall and weighs 75-pounds. The 75-pound weight will be fixed to the top of the inflatable trapezoid. The top and bottom of the trapezoid have rigid platforms glued to them post production of the inflatable trapezoid. The primary movement will not be a yaw in any direction but a bounce up and down movement.
I like math and all this but having a hard time to which rules and principles I should get familiar with before chatting with an engineer.
I like math and all this but having a hard time to which rules and principles I should get familiar with before chatting with an engineer.