Reverend Shabazz
- 19
- 1
Hello, I am reading a section in Jackson discussing classical Rutherford scattering, and he mentions incorporating a cutoff in the Coulomb interaction in order to model electric screening. I am trying to understand how he applies this, as described below.
The set up is basically the classic Rutherford scattering set up with charges ##ze## and ##Ze## interacting with a small angle of deflection (i.e ##sin(\theta/2) \approx \theta/2##), leading to a differential scattering cross section of:
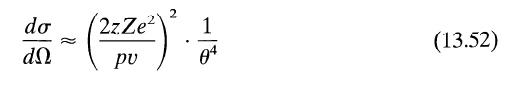
Now at ##\theta=0## of course the cross section is infinite, so he suggests modifying the Coulomb force interaction so as to drop off suddenly at ##r=a##:

So I am trying to understand how he obtains eq. 13.53...or at the very least what the set up is.
My guess is that he starts with a massive incident particle approaching a less massive target particle located at the origin. The massive incident particle is assumed to remain in a straight line, while the target particle deflects. But unlike the typical straight line approximation for this scenario, the typical Coulomb interaction remains the same only within a sphere of radius ##r=a## centered either on the origin or on the particle, beyond which the force is 0. Does this sound right?
Unfortunately, I couldn't find much on the internet pertaining to this question except for an article that I don't have access to: https://aapt.scitation.org/doi/10.1119/1.1987568
The set up is basically the classic Rutherford scattering set up with charges ##ze## and ##Ze## interacting with a small angle of deflection (i.e ##sin(\theta/2) \approx \theta/2##), leading to a differential scattering cross section of:
Now at ##\theta=0## of course the cross section is infinite, so he suggests modifying the Coulomb force interaction so as to drop off suddenly at ##r=a##:
So I am trying to understand how he obtains eq. 13.53...or at the very least what the set up is.
My guess is that he starts with a massive incident particle approaching a less massive target particle located at the origin. The massive incident particle is assumed to remain in a straight line, while the target particle deflects. But unlike the typical straight line approximation for this scenario, the typical Coulomb interaction remains the same only within a sphere of radius ##r=a## centered either on the origin or on the particle, beyond which the force is 0. Does this sound right?
Unfortunately, I couldn't find much on the internet pertaining to this question except for an article that I don't have access to: https://aapt.scitation.org/doi/10.1119/1.1987568