Inducing EMF Through a Coil: Understanding Flux

[Cardinalmont]

Thank you for reading my post. I can understand why a change in magnetic flux through a conducting surface would induce an emf, but how does this work when inducing an emf through a coil? How does the flux through the empty space between the wires have an effect on the electrons in the wire itself?

In the image below is a coil with a magnetic field going through the space between the wires but not necessarily through the wires themselves.

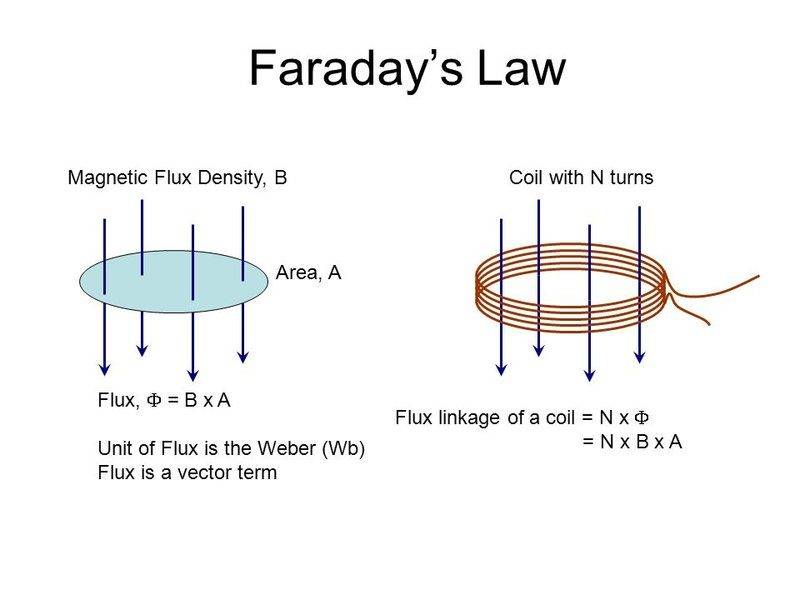
Thank you.

 

[phyzguy]

If there is a magnetic field inside the coil, but the magnetic field where the wires are is zero, then there is no way the flux through the coil can change. It is the change in flux that induces the EMF. In order for the total flux through the coil to change, some magnetic field lines need to cross the coil.

 

[Charles Link]

In some ways, it may seem rather odd that this is how it works, but it is, what it is. Faraday's law in differential form is $\nabla \times E=-\frac{\partial{B}}{\partial{t}}$, and when Stokes law is applied and it is integrated over an area, it becomes $\mathcal{E}=-\frac{d \Phi}{dt}$. They figured out most of this stuff from the period around 1860-1880. I think it took a lot of work on their part to make heads and tails of all of this stuff.

 

[Charles Link]

If there is a magnetic field inside the coil, but the magnetic field where the wires are is zero, then there is no way the flux through the coil can change. It is the change in flux that induces the EMF. In order for the total flux through the coil to change, some magnetic field lines need to cross the coil.

I disagree with this statement. The magnetic flux acts remotely. It doesn't need to cross the wires of the coil.

 

[Cardinalmont]

Also, now that I'm really looking at this image, which is the first image on google when I searched "magnetic flux linkage," I notice that it specifically says "flux is a vector term", when magnetic flux is actually a scalar quantity in this context. Jeez...

 

[phyzguy]

I disagree with this statement. The magnetic flux acts remotely. It doesn't need to cross the wires of the coil.

In the case where B(t) = 0 at the location of the coil, explain to me how the flux Φ of B through the coil can change.

 

[Charles Link]

In the case where B(t) = 0 at the location of the coil, explain to me how the flux Φ of B through the coil can change.

One experimental example is a long current carrying solenoid of radius $a$, and a loop of radius $b$, where $b>a$, and the loop is around the solenoid. For a very long solenoid, for most practical purposes, the magnetic field is completely inside the solenoid and along its axis. If the current in the solenoid is made to vary with time, the magnetic field of the solenoid, which basically is inside of $r<a$, will change, and the loop of radius $b$ will experience an EMF. (The lines of flux will emerge from the solenoid and come back around, but in the vicinity of the loop, the magnetic field is very weak).

 

[phyzguy]

Also, now that I'm really looking at this image, which is the first image on google when I searched "magnetic flux linkage," I notice that it specifically says "flux is a vector term", when magnetic flux is actually a scalar quantity in this context. Jeez...

The flux is : $\Phi = \int \vec{B} \cdot \vec{dS}$ This is a scalar.

 

[phyzguy]

One experimental example is a long current carrying solenoid of radius $a$, and a loop of radius $b$, where $b>a$, and the loop is around the solenoid. For a very long solenoid, for most practical purposes, the magnetic field is completely inside the solenoid and along its axis. If the current in the solenoid is made to vary with time, the magnetic field of the solenoid, which basically is inside of $r<a$, will change, and the loop of radius $b$ will experience an EMF. (The lines of flux will emerge from the solenoid and come back around, but in the vicinity of the loop, the magnetic field is very weak).

If all of the magnetic field lines "loop back around" inside the radius b, then the flux of B through the large coil doesn't change and there is no EMF induced. It's not possible for Φ to change unless some B field lines cut the loop.

 

[Charles Link]

If all of the magnetic field lines "loop back around" inside the radius b, then the flux of B through the large coil doesn't change and there is no EMF induced. It's not possible for Φ to change unless some B field lines cut the loop.

The lines of flux simply need to cut through the plane of the loop, inside the loop. They don't need to cross the wires at all. It would be possible for $B$ to remain zero always and everywhere on the wires themselves, and an EMF would still be generated.

 

[Cardinalmont]

The lines of flux simply need to cut through the plane of the loop, inside the loop. They don't need to cross the wires at all. It would be possible for $B$ to remain zero always and everywhere on the wires themselves, and an EMF would still be generated.

Yes but my original question is "why?" I'm preparing to teach electromagnetic induction and I want to have a really solid understanding before I start.

 

[Charles Link]

Yes but my original question is "why?" I'm preparing to teach electromagnetic induction and I want to have a really solid understanding before I start.

There doesn't seem to be a good answer for why. They discovered this is how it is. The magnetic field can and often does act remotely in generating an EMF. Somewhat peculiar and different from most other things we encounter, but that's what it does.

 

[tech99]

There doesn't seem to be a good answer for why. They discovered this is how it is. The magnetic field can and often does act remotely in generating an EMF. Somewhat peculiar and different from most other things we encounter, but that's what it does.

Doesn't the varying magnetic field produce an electric field and that causes the electrons in the wire to move?
(I am not sure when you say EMF if you mean Electromagnetic Force or Electromagnetic Field, by the way).

 

[Charles Link]

Doesn't the varying magnetic field produce an electric field and that causes the electrons in the wire to move?
(I am not sure when you say EMF if you mean Electromagnetic Force or Electromagnetic Field, by the way).

EMF (electromotive force) $\mathcal{E}=\int E_{induced} \cdot ds$, and around a closed loop, $\mathcal{E}=-\frac{d \Phi}{dt}$, where $\Phi$ is the magnetic flux inside the loop and in the plane of the loop. The $E_{induced}$ can be non-zero even in regions where there is zero magnetic field $B$, e.g. where there is zero magnetic field passing into the wires in which the EMF is generated. The changing $B$ is able to remotely generate a non-zero $E_{induced}$. $\\$ @phyzguy previously questioned this result, so can I ask @vanhees71 to give an input here, in regards to posts 4,6, 7, 9 and 10, 11, and 12. I'm pretty sure I have it correct, but it's always good to get some concurrence.

 

[phyzguy]

EMF (electromotive force) $\mathcal{E}=\int E_{induced} \cdot ds$, and around a closed loop, $\mathcal{E}=-\frac{d \Phi}{dt}$, where $\Phi$ is the magnetic flux inside the loop and in the plane of the loop. The $E_{induced}$ can be non-zero even in regions where there is zero magnetic field $B$, e.g. where there is zero magnetic field passing into the wires in which the EMF is generated. The changing $B$ is able to remotely generate a non-zero $E_{induced}$. $\\$ @phyzguy previously questioned this result, so can I ask @vanhees71 to give an input here, in regards to posts 4,6, 7, 9 and 10, 11, and 12. I'm pretty sure I have it correct, but it's always good to get some concurrence.

And I still disagree with what you are saying. If I have a loop and some flux $\Phi$ of magnetic field through the loop, it is not possible for $\Phi$ to change unless some magnetic field lines pass through the loop. This cannot happen if B is zero everywhere in the loop. I also would like to hear what someone else like @vanhees71 has to say.

 

[Charles Link]

And I still disagree with what you are saying. If I have a loop and some flux $\Phi$ of magnetic field through the loop, it is not possible for $\Phi$ to change unless some magnetic field lines pass through the loop. This cannot happen if B is zero everywhere in the loop. I also would like to hear what someone else like @vanhees71 has to say.

Another experimental example is a solenoid that is toroidal, and you can even put iron inside of it to enhance the magnetic field considerably. The magnetic field is very small outside of the toroid, but you could generate very large EMF's in a loop that goes around the toroid and loops through the hole in the donut, by making the current sinusoidal in time. (Many transformers have a similar design). $\\$ Yes, @vanhees71 , we need your input please. :)

 

[vanhees71]

I don't understand the problem really well. Is it about the usual transformer setup, where you have some "soft iron" core and two coils wound around. If you put an AC current at one coil, you have a time-varying magnetic field, which thanks to the iron core is quite localized in the core. Since it's time varying a electric vortex field is induced according to (I try the SI, because in the next semester, I've to give a lecture for teachers' students, where I have to use the SI):
$$\vec{\nabla} \times \vec{E}=-\partial_t \vec{B}.$$
You get the electromotive force in the secondary coil by using Stokes's integral theorem using an arbitrary surface cutting the iron core with the boundary given by the coil (don't forget to multiply by the winding number $N_2$ of the coil, i.e.,)
$$\mathcal{E}_2=\int_{\partial a_2} \mathrm{d} \vec{r} \cdot \vec{E}=-N_2 \dot{\Phi}_B.$$
This must be equal to the electromotive force in the primary coil, from which you get
$$\mathcal{E}_2=\frac{N_2}{N_1} \mathcal{E}_1.$$

 

[Charles Link]

Hello @vanhees71 This was somewhat helpful, but the question is, can the magnetic field of the primary coil be exactly/nearly zero at all times at the radius of the secondary coil, call it at $r=b$ to $r=b+\Delta b$, i.e. can we confine the magnetic field of the primary to $r<a+\Delta a$, (where $r+\Delta a <b$) and still generate the EMF in the secondary coil?$\\$ e.g. Let $a=1"$ and $b=2"$. The magnetic field $B(r)$ is then nearly zero for $r>1.1"$. My claim is that $B(r=2") \approx 0$ for this problem at all times, (in principle $B(r=2")=0$), even though $E_{induced}(r=2")$ is non-zero. $\\$ Large regions of non-zero $E_{induced}$ seem to get created by what can be a very localized region of magnetic field $B$ that undergoes a change in time. In the case of a toroid, my claim is that the magnetic field can be confined to the interior of the toroid, and we get plenty of $E_{induced}$ outside the toroid if we cause the magnetic field to change inside the toroid.

 

[tech99]

Hello @vanhees71 In the case of a toroid, my claim is that the magnetic field can be confined to the interior of the toroid, and we get plenty of $E_{induced}$ outside the toroid if we cause the magnetic field to change inside the toroid.

This claim seems correct. In fact, with a toroid, a straight wire passing through it will still have the same voltage induced as a small turn. The straight wire is in a circuit which forms a huge loop. It does not matter how big the turn is, the voltage will be the same. I am not sure if Maxwell's Equations actually say this.

 

[vanhees71]

If Maxwell's equations don't say, then it is wrong almost with certainty. As long as no quantum effects are relevant, Maxwell's electromagnetics (including optics!) is the most accurate theory ever!

 

[Charles Link]

Maxwell's equations say it with $\nabla \times E=-\frac{\partial{B}}{\partial{t}}$ along with Stokes theorem to give EMF $\mathcal{E}=\int E \cdot ds=-\frac{d \Phi}{dt}$.

 

[vanhees71]

The differential form is correct, the integral form only if there are no moving parts in your surface and boundary. The correct integral form is (in SI units)
$$\frac{\mathrm{d} \Phi_B}{\mathrm{d} t}=\frac{\mathrm{d}}{\mathrm{d} t} \int_A \mathrm{d}^2 \vec{f} \cdot \vec{B}=-\mathcal{E}=\int_{\partial A} \mathrm{d} \vec{r} \cdot (\vec{E}+\vec{v} \times \vec{B}).$$
Here $\vec{v}$ is the velocity of the boundary $\partial A$ of the surface $A$ used to define the magnetic flux.

 

[end541]

I have an explanation: when the flux that does cut the wire of the coil induces EMF an electric field, and so a magnetic field, is included. This field is affected by the empty space inside of the coil, and so the coil's own magnetic field is varied, thereby including EMF from the flux cut in the empty area inside of the coil

 

[nasu]

And I still disagree with what you are saying. If I have a loop and some flux $\Phi$ of magnetic field through the loop, it is not possible for $\Phi$ to change unless some magnetic field lines pass through the loop. This cannot happen if B is zero everywhere in the loop. I also would like to hear what someone else like @vanhees71 has to say.

Can you specify what do you mena when you say "through the loop"? Usually this means through the area delimited by the contour of the loop. Is this what you mean? Or you rather mean through the metallic wire going around this area?

 

[vanhees71]

Of course, if the electric field across the surface $A$ is 0 all the time, the magnetic flux through the surface is 0, and so is the electromotive force. See #22, where the complete integral form of Faraday's law for moving surfaces and boundaries is given.

 

[Mohamed Ijaz]

I don't understand the problem really well. Is it about the usual transformer setup, where you have some "soft iron" core and two coils wound around. If you put an AC current at one coil, you have a time-varying magnetic field, which thanks to the iron core is quite localized in the core. Since it's time varying a electric vortex field is induced according to (I try the SI, because in the next semester, I've to give a lecture for teachers' students, where I have to use the SI):
$$\vec{\nabla} \times \vec{E}=-\partial_t \vec{B}.$$
You get the electromotive force in the secondary coil by using Stokes's integral theorem using an arbitrary surface cutting the iron core with the boundary given by the coil (don't forget to multiply by the winding number $N_2$ of the coil, i.e.,)
$$\mathcal{E}_2=\int_{\partial a_2} \mathrm{d} \vec{r} \cdot \vec{E}=-N_2 \dot{\Phi}_B.$$
This must be equal to the electromotive force in the primary coil, from which you get
$$\mathcal{E}_2=\frac{N_2}{N_1} \mathcal{E}_1.$$

Simple: the time-varying magnetic field inside the coil produces a time-varying electric field that permeates through the core to the outside. And this time-varying electric field outside the core produces a time-varying magnetic field outside the core which interacts with the coil outside! (This is a conceptual way to visualize this)!

 

[Charles Link]

See: https://www.physicsforums.com/threa...duction-lecture-16.948122/page-6#post-6857043
You might find this thread of interest=look at in particular posts 187, 188, 189, and 194. There doesn't seem to be complete agreement in the Physics Forums regarding this topic, but you still may find this of interest. It is up to the individual to ultimately determine what is good physics and what isn't.

Note: I got the necessary edits in to these posts before the thread was closed. I stick by my conclusions on this. We don't have complete agreement with everyone, but that is ok.

 

[alan123hk]

And I still disagree with what you are saying. If I have a loop and some flux Φ of magnetic field through the loop, it is not possible for Φ to change unless some magnetic field lines pass through the loop. This cannot happen if B is zero everywhere in the loop. I also would like to hear what someone else like @vanhees71 has to say.

I think I might understand your argument. Why does magnetic flux through a coil induce an emf without actually touching or cutting the coil wires? From a logic and reasoning standpoint, this is a little unbelievable. I noticed that the integral form of Faraday's law does not seem to contain information about the distance between the magnetic flux (situation discussed now is coil wire) and the integral curve, but in fact if there is a separation distance between them, it must take time to transmit the information about the change of magnetic flux to the the coil wire.

So I think the information about the change in magnetic flux is transmitted to the the coil wire in the form of a time-varying electromagnetic field, and there is a certain delay time. The transmission speed in vacuum is the speed of light.

Generally speaking, when we use the integral form of Faraday's law, we assume that the distance is much smaller than the wavelength of the operating frequency, so we ignore this time delay effect.

 

[Charles Link]

The ideal very long solenoid has a uniform magnetic field inside it in the z direction, and zero magnetic field outside of it. Experimentally, a very predictable EMF results in a loop of wire external to the solenoid that encompasses the solenoid if the current in the solenoid changes, resulting in a change in the magnetic field inside the solenoid. For all practical purposes, there is zero magnetic field in this external loop of wire.

Faraday's law for the EMF, $\mathcal{E}=- \frac{d \Phi}{dt}$, which is the Maxwell formula $\nabla \times E =-\dot{B}$, integrated over an area along with Stokes' theorem, works with very high precision. I don't have a good explanation though for how and why the changing magnetic field is able to act very non-locally, creating the EMF in a very predictable manner.

 

[alan123hk]

For all practical purposes, there is zero magnetic field in this external loop of wire

So even though I say that information about changes in the magnetic field is transmitted to the coil wires, that might be a little misleading. I agree with your point about short-range electromagnetic induction applications, such as the paradigm we discuss here, where there is no measurable magnetic field at all in the external coil. Even if a magnetic field exists, its strength is too weak to measure.

 

[Charles Link]

It might be of interest at this point to look more closely at the EMF that gets generated when a loop containing $N$ coils is introduced. We could just use Faraday's law with the flux being $N$ times as much, but I did notice there is a way to explain this using the $E_{induced}$. See https://www.feynmanlectures.caltech.edu/II_22.html
This one is subject to some interpretation, but right after equation (22.3) Feynman says there can be no electric fields inside an ideal conductor. I interpret that as saying there arises an $E_{s}$ in the conductor, where $E_s=-E_{induced}$. This $E_s$ will integrate along the path inside of the coil to give it the factor of $N$ times the EMF of a single loop. In addition, external to the $N$ loops, it must also give this same result, since $\nabla \times E_s =0$. This (the electrostatic component) is what I believe we measure with a voltmeter when we measure the EMF from the coil. See also post 27 above and the thread that is linked. In private discussions (PM) with others, I don't have complete agreement on this, but perhaps you @alan123hk might concur. The connections of the leads to the voltmeter can be close enough together that we clearly aren't measuring the $E_{induced}$, but the integral $\int E_s \, dl$ between two points must be path independent, and thereby gives the same result that it does going through the voltmeter and voltmeter leads, as it does through the coil, resulting in a very reliable voltage measurement.

Then there is also the case of a single loop that is open, the subject of the Walter Lewin paradox, where it matters which side of the localized changing magnetic field the voltmeter is placed, but that is a separate problem, and it has already been discussed in detail. For that case, the voltmeter is also seeing $E_{induced}$, and how much (integral of) $E_{induced}$ that is observed (depends on location of the meter) makes a difference in the measurement.

For $N$ in the above, the location of the meter could make it $N \pm 1$, etc., which usually doesn't have a significant effect in the voltage reading, provided $N$ is fairly large.

See also https://www.physicsforums.com/threa...-voltage-across-inductor.880100/#post-5529838 post 22.

 

[alan123hk]

I interpret that as saying there arises an Es in the conductor, where Es=−Einduced. This Es will integrate along the path inside of the coil to give it the factor of N times the EMF of a single loop. In addition, external to the N loops, it must also give this same result, since...=0 ... perhaps you @alan123hk might concur

Yes, I very much agree with your previous analysis, you explained very well why the induced emf is proportional to the number of turns of the coil.

The connections of the leads to the voltmeter can be close enough together that we clearly aren't measuring the Einduced, but the integral ∫Esdl between two points must be path independent, and thereby gives the same result that it does going through the voltmeter and voltmeter leads, as it does through the coil, resulting in a very reliable voltage measurement.

As described in Feynman's lectures https://www.feynmanlectures.caltech.edu/II_22.html
"we have assumed that there are no magnetic fields in the space outside of the “box,” this part of the integral is independent of the path chosen and we can define the potentials of the two terminals"

Just like the AC voltage provided by the power company, users obtain stable AC voltage independent of the transmission line path through the transmission cables outside the power company's substation facilities.

Please note that the user does not have the means or right to go into the power company facility and put extra turns of wire on the transformer to change the voltage.

 

[Charles Link]

Yes, I very much agree with your previous analysis, you explained very well why the induced emf is proportional to the number of turns of the coil.

Very good. :)

It should be noted that in some previous discussions on PF where $E_s=-E_{induced}$ in the conductor was introduced, (by another member), one major criticism was presented of
how can a non-conservative field ($E_{induced}$) be the opposite of and basically be represented by a conservative field ($E_s$)?
If $\nabla \times E_{induced}=-\dot{B}$, it should be impossible to have $E_s=-E_{induced}$ (in the conductor) with $\nabla \times E_s=0$.

It looked like it could be a valid objection, but then I later saw the explanation: When you go once around the loop (of the $N$ turn coil) $\oint E_{induced} \, dl=-\dot{\Phi}$. When you go once around the same path with $\oint E_s \, dl$, you get $\dot{\Phi}$ rather than zero, (even though $\nabla \times E_s=0$), because you are now in the adjacent ring of the coil.

Likewise if you go around $N$ times, you then have traversed the entire coil, and get $\int E_s \, dl=N \dot{\Phi}=EMF$ rather than zero. Thereby, we still have a conservative field $E_s$, so the path integral outside through the voltmeter between the two ends of the coil also gives the same EMF, but where the coil boundaries gave us the special property where $\oint E_s \, dl$ could be non-zero.

@alan123hk The above is a little extra work, but you may find it of interest.

Note: It took a little proof-reading and a couple edits, but I think I now have it reading like it should. :)

 

[alan123hk]

If ∇×Einduced=−B˙, it should be impossible to have Es=−Einduced (in the conductor) with ∇×Es=0.

above is a little extra work, but you may find it of interest.

I have also thought about this issue, here are my thoughts

There may not necessarily be an induced electric field with curl inside the wires of the coil. If the changing magnetic flux only concentrated at the center of the coil and does not pass through the coil wire, then the induced electric field in the wire should have no curl, at this time, the electric field generated by the accumulated charge can completely offset the induced electric field, so the electric field inside the wire becomes zero.

Even if the magnetic flux passes through the wire of the coil and a curly electric field appears inside the wire, the electric field generated by the accumulated charge cannot and does not necessarily completely cancel the curly electric field. All it has to do is make the line integral of the electric field along the coil wire zero. The effect should be very close to before. The voltage across the coil remains unchanged, complying with Faraday's law. However, strong eddy currents will be generated inside the coil wires, causing greater losses.

 

[Charles Link]

It may be worthwhile at this time to consider the very ideal case that $\dot{B}$ is uniform (in the z direction) inside a small circular cylindrical region of basically infinite length, (the ideal very long solenoid discussed above, with a changing current (changing at a constant rate) in its windings), and with $\dot{B}$ essentially zero everywhere else.

We do find that to have $\nabla \cdot B=0$,(magnetic flux is conserved), the integrals of $B$ and $\dot{B}$ over the infinite area outside of this region need to be finite, even though $B$ and $\dot{B}$ are essentially zero.

Outside of this circular region we have that $\nabla \times E=-\dot{B}=0$, but that does not mean that $E=0$. Instead we can use Stokes' law, along with symmetry and get that $\oint E_{induced} \cdot \, dl=-\dot{\Phi}=2 \pi r E_{induced}$, (vector direction should be apparent, but is omitted), so that we can accurately compute $E_{induced}$ as a function of $r$ for this case.

It's the very ideal case, and kind of a simple example, but it may be worthwhile taking a close look at it.