Satellite Orbit synchronization

[Ibix]

This simpler setup still captures what I think is the essence of @name123's problem: How can it be that all the satellites log the same arrival time for the flashes, and their clocks match when they meet every half-orbit, even though the clocks on the satellites are mutually time-dilated so that the satellite observers will always find all the other satellite clocks to running slow for the entire orbit?

Indeed. So we have two co-axial counter-rotating merry go rounds with clocks on their rims. I think the only real difference this makes to my answer is that the maths of working out what each clock actually sees from a counter-rotating clock is merely annoying, not actively difficult.

In particular, chaining together local Einstein frames still fails, and for the same reason. Global inertial frames are available, but any chosen clock is only instantaneously at rest, or never at rest, in any chosen one.

 

[Dale]

This simpler setup still captures what I think is the essence of @name123's problem

I agree, that is a much better problem. Of course, even in flat spacetime there is not one unique definition of the reference frame for a non-inertial observer. So the OP will still need to specify what reference frame he wants to use to indicate the satellite's reference frame as a transformation from some inertial frame.

 

[name123]

well as with any scenario where you have relative motion, you do have to take the relativity of simultaneity in account.
To demonstrate we will just consider linear motion.
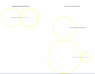
Below is a rod from which light flashes initiate at the ends To the left is how events occur according to the rod itself. The flashes start at the same time and the expanding light meets at the center of the rod.
On the right are the same events according to someone for which the rod is moving at 0.5c to the right.
The flash from the left end of the rod starts first, and the light expands outward at c while the rod continues to move to the right.
After the rod has moved some distance, the second flash leaves the right end, and expands out at c. Both flashes continue to expand as the rod continues to move to the right until they meet, again at the middle of the rod.
View attachment 228688
The fact that the light meets at the center of the rod is an invariant fact for both frame. Whether or not each flash started at the same time is not.
So in your scenario, the fact that flashes from the spacecraft arrive at all the satellites simultaneously in one frame does not mean that they arrive simultaneously in all frames. In the same way, the fact that two satellites are always in sync when they pass each other is an invariant fact doesn't mean that they remain in sync at all points of their orbits in all frames.

I had already explained in post #43 how I was visualising it. And there it was clear that I was not thinking that from a satellite's perspective all the satellites were receiving the signal at the same time (because their distance to the shapeship flashing would be different). My surprise with your visualisation in post #55 was that you were envisaging length contraction not just in the x direction, but also in the y direction perpendicular to it. I did not realize there would be length contraction in the y direction also. I was imagining it without length contraction in the y direction, and wondered how if there was no length contraction in the y, such that the satellites either side of the satellite opposite the one whose perspective it is where the same distance from the spaceship as the ones either side of the satellite whose perspective it is, how it could be explained them receiving the light at the same time if they were thought to be in the position you depicted. So a confusion on my part. The answer presumably being that there would be considered to be length contraction in the y. Anyway, as I mentioned I did not realize there would be length contraction in the y direction as it isn't mentioned in the special relativity equations.

Anyway, my surprise there does not effect the part that I was confused about and mentioned in #43:

The problem I would have with it is that if their clocks are going slower how do they show the same time per orbit. Could you perhaps explain it in terms of mathematical example, or explain conceptually the error I made? I imagine it as rotating a cardboard cutout around an axis, (different spoke lengths for different satellites) but having a problem of the clocks on some satellites (rather than their velocities) going slower than others but measuring the same time per orbit.

I don't need a mathematical example, or the exact figures, I would be happy with someone just pointing out what was wrong with the visualisation of the problem (the contraction in the y-direction doesn't alter the problem I have with the conception).

 

[Nugatory]

Just to be clear what I mean is that if in your chosen frame of reference each satellite receives each light flash from the spaceships at the same time, and at that time (according to your calculations for that frame of reference) some of their clocks were going at different rates to other ones, then how comes when they come to log the time they detected the flash of light they all report the same time on their clocks.

We are using coordinates in which the Earth and the two spaceships are at rest. This is an inertial frame in which all the satellites are moving as they orbit; because it is an inertial frame the speed of light is always $c$. Using these coordinates, the distance from either spaceship to any of the satellites is the same, so the light travel time from spaceship to satellite is the same for all the satellites. All of the satellite clocks are running slow, meaning that at the same time that the spaceship/earth clocks read $T$ the satellite clocks read $T-\Delta$; thus if a flash reaches a satellite at the same time that the earth/spaceship clocks read $T$ the timestamp logged by the satellite will be $T-\Delta$. However, it turns out that the value of $\Delta$ is the same for all the satellites (which is not at all surprising when you consider that they're all moving at the same speed relative to Earth so you'd expect the same amount of time dilation). Because the value of $\Delta$ is the same for all the clocks (equivalently, the clocks are all slow by the same amount) they all end up with the same timestamps.

So far we're fine, there's not even a hint of an apparent paradox in any of this. Furthermore, we're happy with the idea that the clocks on the orbiting and counter-orbiting satellites will agree when they pass each other - just consider that a flash of light arriving at two satellites at the moment that they're passing one another will get the same timestamp.

The apparent contradiction you're seeing appears when we use the procedure I described in post #30 to compare the rate at which the clock on one satellite ticks with the rate of a clock on another satellite. How can the timestamps all match, and the clocks match when the rotating and counter-rotating satellites meet at every orbit, when the clocks are always running at different rates? That's where the relativity of simultaneity comes in.

A few paragraphs back I said that "at the same time that the spaceship/earth clocks read $T$ the satellite clocks read $T-\Delta$" - and relativity of simultaneity means that things that happen at the same time in one frame may not happen at the same time in another frame. We're using the frame in which the Earth and the two spaceships are at rest and we find that all the satellite clocks read $T-\Delta$ at the same time; but when we use the procedure of post #30 we're using a different frame (the inertial frame in which satellite X is momentarily at rest) and in this one the events "satellite X clock reads $T-\Delta$" and "satellite Y clock reads $T-\Delta$ do not happen at the same time. However, in this frame the distances between the spaceships and the two satellites are also not the same so the light travel time is also different; the two effects cancel each other out so that the timestamps end up the same. So that's how the timestamps come out the same even though the clocks aren't synchronized.

Relativity of simultaneity will also explain how the clocks on satellite X and satellite Y end up agreeing when they pass one another but the explanation is a bit harder to visualize; you are probably better off starting with the "Doppler explanation" section of this FAQ. The situation is different because we're dealing with a complicated circular path instead of straight-line out and back paths, but the result has to be the same: the total number of flashes that reach X from Y in a half-orbit has to be equal to the total number of flashes X emits during that half orbit; the two clocks tick once with for every flash, so they both have to tick off the same amount of time during their half-orbits between one meeting and the next.
Now consider the situation on satellite X $t$ seconds before it passes satellite Y with both of their clocks reading $T$; clearly X's clock reads $T-x$. However, at the same time (using the frame in which X is momentarily at rest) that X's clock reads $T-x$ the clock on satellite Y will not read $T-x$; it reads some value that added to the number of time Y's clock will tick as it finishes its half-orbit will be equal to $T$. (If you are not familiar with the "Andromeda paradox", google for it - the small changes in the relative speed of X and Y as they orbit make for large and counterintuitive changes in what they are doing "at the same time").

 

[Dale]

I had already explained in post #43 how I was visualising it. And there it was clear that I was not thinking that from a satellite's perspective all the satellites were receiving the signal at the same time (because their distance to the shapeship flashing would be different).

The problem with your description of post 43 is that you were describing a lot of features and details that you assumed that "the satellite's frame" would have without actually writing down what you mean by "the satellite's frame" and showing that it actually has those features. There is simply no way to avoid it. The satellites are non-inertial, so there is no default frame to use that we consider to be their frame. You actually have to specify it explicitly, e.g. as a transform between the ship's frame which is inertial.

Basically, you are asking a question with a crucial undefined term in it. You are struggling to understand the answers, but you need to work on understanding your own question first. Work on the question first, that is, work on defining what you mean exactly by "the satellite's frame".

 

[name123]

I thought it was obvious in post #43 I was considering that the satellite's perspective could be approximated by imagining a series of short lines where it is traveling at the velocity it is in the direction of it's tangent. Each consideration could be of a duration of 0.0000000000000000000000000000000000000000001 nanoseconds while the orbit could be a billion years. I had described how such a configuration would lead to the imagining of the situation, and it would not be too different from that considered by Janus in post #55

Assuming you had a spaceship( the red arrow in the following image) skimming the orbit of a ring of satellites such that it momentarily matches the velocity of the satellite it is passing, then,...

Except I had not imagined any length contraction in the y direction. If you think both my and Janus's consideration that the orbits of the other satellites would appear elliptical is wrong, then please say so. If not then the point I am making stands. As it goes around, a satellite (in the same series) appearing to be closer to the centre of the sphere/spheroid would seem to remain at that distance the whole way around. Which would mean the light from the spaceship flashes would have taken less time to reach it. It could then be concluded that it's clocks were going slower because they register the same time reading for the light reaching them. What I am having trouble with is the reconciliation of the clocks being considered as going slower on the other satellite the whole orbit, and the orbit being measured as taking the same time according to their clock, and the satellite never overtaking. The reason is that if their clock was going slower, then the observing satellite would presumably be concluding that the orbit took less time than the slower clock showed, but if it were orbiting in less time than the observing satellite was orbiting then why does in not do more orbits over a long period?

 

[jbriggs444]

series of short lines

The short lines are not a problem. The bends between the short lines are. They have to be accounted for. Each bend changes the simultaneity convention used between the one tangent inertial frame and the next.

 

[name123]

The short lines are not a problem. The bends between the short lines are. They have to be accounted for. Each bend changes the simultaneity convention used between the one tangent inertial frame and the next.

So is it that you think both my and Janus's consideration that the orbits of the other satellites would appear elliptical from the satellite's perspective is wrong? If then please say so. If not then I am not sure what difference you are thinking it makes to the problem I mentioned. Perhaps you could explain.

 

[Dale]

If you think both my and Janus's consideration that the orbits of the other satellites would appear elliptical is wrong, then please say so.

Yes, I think it is wrong. You cannot make a valid non-inertial frame by stitching together a bunch of inertial frames. When we say "the satellite's perspective" in relativity then we are talking about a reference frame where the satellites are at rest. Since they are non-inertial then there is no standard reference frame and it must be explicitly defined. A sequence of inertial frames does not represent the satellite's frame.

 

[name123]

Yes, I think it is wrong. You cannot make a valid non-inertial frame by stitching together a bunch of inertial frames. When we say "the satellite's perspective" in relativity then we are talking about a reference frame where the satellites are at rest. Since they are non-inertial then there is no standard reference frame and it must be explicitly defined. A sequence of inertial frames does not represent the satellite's frame.

Ok, well however it would look for satellites of its own series, do you accept that it would look that way the whole way around given the symmetry?

 

[Dale]

Ok, well however it would look for satellites of its own series, do you accept that it would look that way the whole way around given the symmetry?

Only if you define the transformation that way! You can define it largely arbitrarily, so it is up to you to include that feature if you see it as an important feature to include. This is something that is up to you to decide, and you do that by specifying the satellite's reference frame mathematically.

 

[name123]

Only if you define the transformation that way! You can define it largely arbitrarily, so it is up to you to include that feature if you see it as an important feature to include. This is something that is up to you to decide, and you do that by specifying the satellite's reference frame mathematically.

Just to be clear what I meant, is that at no matter what part of the orbit the satellite is, its observational relationship to the other satellites in its series does not change. So that if there were no defining features on the "sphere" and no other things in the universe other than those being considered, you could not tell from photographs which part of the orbit the satellite was in. If you were already clear on that, then I am not sure what is arbitrary about it. Perhaps you could give an example of how it is arbitrary?

 

[Ibix]

Ok, well however it would look for satellites of its own series, do you accept that it would look that way the whole way around given the symmetry?

You want to know what a satellite's clock shows at the same time as another satellite's clock reads 00.01, 00.02, 00.03 etc.

1. In relativity there is no general meaning to "at the same time".
2. For inertial bodies in flat spacetime there is a sensible default guess as to what "at the same time" means (Einstein frames).
   
3. This scenario is either not in flat spacetime (your formulation) or the satellites are not inertial (Nugatory's formulation).
4. Thus there is no default sensible meaning to "at the same time".
5. The only attempt you've made to define "at the same time" (chaining together small inertial frames) does not produce a consistent meaning (see post #69).
6. You are free to define "at the same time" in many different ways. Pretty much the only constraints are that the other satellite's clock must always be advancing and we must not assign two times to the same event. The rate depends on your definition.
7. Since you don't have a definition of "at the same time" forced on you or pre-selected by some mechanism then the question is pointless. The answer is "whatever you define it to be".

Can you tell us what step in that chain of reasoning is escaping you?

 

[PeterDonis]

I thought it was obvious in post #43 I was considering that the satellite's perspective could be approximated by imagining a series of short lines where it is traveling at the velocity it is in the direction of it's tangent.

If this was what you were thinking, unfortunately, it's not correct. You cannot construct a valid global frame this way.

 

[Dale]

Perhaps you could give an example of how it is arbitrary?

Yes, you have the freedom to define the transformation as something like:
$t=\gamma T$
$r=R$
$\phi=\Phi+\omega T$
$z=Z$
or
$t=\gamma T$
$x= X \cos(\Phi+\omega T) + \gamma Y \sin(\Phi+\omega T)$
$y= Y\cos(\Phi+\omega T) - \gamma X \sin(\Phi+\omega T)$
$z=Z$
or
...

It is up to you.

 

[russ_watters]

I What I am having trouble with is the reconciliation of the clocks being considered as going slower on the other satellite the whole orbit...

Again, this is not what happens or is observed. If a satellite is watching another satellite's clock (or via radio), when they are moving apart each will observe the other's clock to be running slower and when they are approaching each will observe the other's clock to be running faster.

@Nugatory provided the details of this in Post #74. I feel like your not wanting to accept this has been your entire issue all along. From the link he provided:

Let us focus on what Stella and Terence actually see with their own eyes. (Just to emphasize that we're talking about direct observation here, I'll put the verb "see" and its brothers in the HTML strong font throughout this section.) To make things interesting, we'll equip them with unbelievably powerful telescopes, so each twin can watch the other's clock throughout the trip. If each twin saw the other clock run slow throughout the trip, then we would have a contradiction. But this is not what they see.

Just in case it's too hard to read the clock hands through the telescope, we'll add a flash unit to each clock, set to flash once a second. You might guess at first that Terence sees Stella's clock flashing once every 7 seconds (with the time dilation factor we've chosen) and vice versa. Not so! On the Outbound Leg, Terence sees a flash rate of approximately one flash per 14 seconds; on the Inbound Leg, he seesher clock going at about 14 flashes per second. That is, he sees it running fast! Stella sees the same behavior in Terence's clock.

 

[Dale]

Again, this is not what happens or is observed. If a satellite is watching another satellite's clock (or via radio), when they are moving apart each will observe the other's clock to be running slower and when they are approaching each will observe the other's clock to be running faster.

Where "observe" refers to the frame invariant Doppler shift rather than some coordinate-dependent quantity.

 

[Ibix]

Where "observe" refers to the frame invariant Doppler shift rather than some coordinate-dependent quantity.

Indeed. If you want to know what a video camera mounted on one satellite and tracking another will actually record, @name123, then that's possible in principle. Even with Nugatory's simplified scenario it would involve numerical approximation, but it's possible. It's just that you can't work backwards to subtract out the Doppler effect without first picking a definition of "at the same time".

 

[name123]

You want to know what a satellite's clock shows at the same time as another satellite's clock reads 00.01, 00.02, 00.03 etc.

1. In relativity there is no general meaning to "at the same time".
2. For inertial bodies in flat spacetime there is a sensible default guess as to what "at the same time" means (Einstein frames).
   
3. This scenario is either not in flat spacetime (your formulation) or the satellites are not inertial (Nugatory's formulation).
4. Thus there is no default sensible meaning to "at the same time".
5. The only attempt you've made to define "at the same time" (chaining together small inertial frames) does not produce a consistent meaning (see post #69).
6. You are free to define "at the same time" in many different ways. Pretty much the only constraints are that the other satellite's clock must always be advancing and we must not assign two times to the same event. The rate depends on your definition.
7. Since you don't have a definition of "at the same time" forced on you or pre-selected by some mechanism then the question is pointless. The answer is "whatever you define it to be".

Can you tell us what step in that chain of reasoning is escaping you?

No you I was not asking what a satellites clock shows at the same time as another satellites clock reads 00.01, 00.02 etc. I had tried to explain what I meant in post #82 when I wrote:

Just to be clear what I meant, is that at no matter what part of the orbit the satellite is, its observational relationship to the other satellites in its series does not change. So that if there were no defining features on the "sphere" and no other things in the universe other than those being considered, you could not tell from photographs which part of the orbit the satellite was in. If you were already clear on that, then I am not sure what is arbitrary about it. Perhaps you could give an example of how it is arbitrary?

You can imagine that the pictures do not give you sight of whether the other satellites (in the same series) have clocks or not.

 

[name123]

Yes, you have the freedom to define the transformation as something like:
$t=\gamma T$
$r=R$
$\phi=\Phi+\omega T$
$z=Z$
or
$t=\gamma T$
$x= X \cos(\Phi+\omega T) + \gamma Y \sin(\Phi+\omega T)$
$y= Y\cos(\Phi+\omega T) - \gamma X \sin(\Phi+\omega T)$
$z=Z$
or
...

It is up to you.

I am not quite clear on what the different symbols mean, but are you suggesting that if one of those transformations were chosen, that you could tell from pictures taken from one of the satellites (imagine none contain clocks, and so no clock can be pictured), that you could tell where it was in its orbit (perhaps from how far apart its neighbouring satellites appeared from it or from the centre of the "sphere")?

 

[name123]

Again, this is not what happens or is observed. If a satellite is watching another satellite's clock (or via radio), when they are moving apart each will observe the other's clock to be running slower and when they are approaching each will observe the other's clock to be running faster.

You seem to have mistakenly thought that I was discussing an A series satellite looking at B series satellite, but I was discussing an A series satellite looking at an A series satellite, as I thought I made clear in the post you were quoting from. At that point I was thinking that the orbits of the A series satellites would appear elliptical as it seems Janus also thought in post #55. But apparently that was wrong. According to Dale in post #79 at least.

If you had thought I was discussing an A series satellite looking at a B series satellite, then I would have thought that the one in front and the one behind appeared the same throughout the orbit, neither seeming to approaching or going away. Are you disagreeing with that?

 

[Ibix]

No you I was not asking what a satellites clock shows at the same time as another satellites clock reads 00.01, 00.02 etc. I had tried to explain what I meant in post #82 when I wrote

The satellites in the same chain always look to be in the same place as seen by one of their number, but this comes under what I said in #88 - you can work out what a camera sees. You still cannot back out from that to get "where they really are now" because "where they really are now" depends on what you mean by "now".

 

[Janus]

My surprise with your visualisation in post #55 was that you were envisaging length contraction not just in the x direction, but also in the y direction perpendicular to it. I did not realize there would be length contraction in the y direction also. I was imagining it without length contraction in the y direction, and wondered how if there was no length contraction in the y, such that the satellites either side of the satellite opposite the one whose perspective it is where the same distance from the spaceship as the ones either side of the satellite whose perspective it is, how it could be explained them receiving the light at the same time if they were thought to be in the position you depicted. So a confusion on my part. The answer presumably being that there would be considered to be length contraction in the y. Anyway, as I mentioned I did not realize there would be length contraction in the y direction as it isn't mentioned in the special relativity equations.

The the image is from the frame of the rocket which is just skimming the orbit, going right to left, while the satellites are orbiting in a clockwise direction. His speed is equal to the orbital speed of the satellite he is passing at the moment. ( the bottom most blue dot. ) As measured from his frame, The satellite he is next to at that moment has a relative speed of 0 with respect to himself . The satellite on the opposite of the orbit would have an a velocity of 2v/(1+v^2/c) assuming v is the orbital velocity. (in Newtonian Physics it would be 2v.)
So let's say that the 0ribital velocity as measured from the center of the orbit is 0.6c. Then the spaceship will measure the velocity of the satellite next to it at that moment to have a relative velocity of 0. and the satellite on the opposite side as having a relative velocity of 0.8826c. (this also means that he will measure the respective speed between these satellites and the center of the orbit as being different.)
Now imagine that each of these satellites has a satellite just leading and just trailing it. as long as they are close to each other, the spaceship can consider each group of three satellites as all having close to an equal velocity with respect to him. ( the near group would all have 0 velocity and the far group would all have a velocity of 0.8826. This means that he will measure no length contraction between the nearby satellites and a length contraction of 0.47. Thus he will measure the distance between the further satellites as being less than that for the nearby satellites (even though if you were to ask the satellites themselves they would all give the same answer as to their distance apart).

But what about the satellites 90° away in the orbit? For the ship, these satellites have two velocity components, 0.6 in the x direction due to the relative velocity between the ship and the center of the orbit, and a component in the y direction due to the satellite's orbital velocity. The y velocity component will work out to be .0.48c. For a group of three satellites at this these points of the orbit, the ship would measure a length contraction between them of 0.877. ( there would also be a 0.8 x-axis length contraction, but since each group of three satellites is in a nearly straight line along the y axis, it wouldn't be easily noticeable.)

So relative to the spaceship frame, the satellites have a mixture of various x and y relative velocities and thus a mixture of x and y-axis length contraction affecting the measured distance between them and the distance between adjacent satellites vary as they travel around an orbit.

Three points of importance:

I'm using the "merry-go-round" model rather than the "orbiting due a gravity field" model to avoid having to deal with the extra complications gravity brings.

This isn't what the spaceship would visually perceive at that moment, rather what he would determine were the positions of those satellites at that moment (by taking what he sees, and working backwards while compensating for light travel time, aberration, etc. )

These are not the relative positions between satellites the the satellite the ship is adjacent to would measure. Even though it is at that moment at rest with respect to the spaceship and seeing exactly the same light, it would come to a different conclusion of how the other satellites are positioned relative to itself.

As already noted, due to the fact that the satellite is in an non-inertial frame (due to its circular motion) and the spaceship is in an inertial frame, the two will come to different conclusions despite the fact that they are momentarily at rest with respect to each other at that moment.
For example, for the spaceship, a clock sitting at the center of the orbit will run slow by a factor of 0.8, but for the satellite, the center clock runs fast by a factor of 1.25.

 

[Dale]

I am not quite clear on what the different symbols mean

Sorry, I should have been clear. The capital letters are coordinates in the ship's inertial frame. The lower case letters are coordinates in some possible examples of the satellite's frame. Don't take these specific transforms too seriously, I was just throwing together examples, not recommending either of them. You need to sit down and decide what specific of all possible transforms you wish to consider when you use the phrase "the satellite's perspective" or "the satellite's frame".

but are you suggesting that if one of those transformations were chosen, that you could tell from pictures taken from one of the satellites (imagine none contain clocks, and so no clock can be pictured), that you could tell where it was in its orbit?

No, I was giving an example of how the reference frames are arbitrary and some may not result in circular orbits. I was not making any claims about pictures or observations, I am still trying to get you to define what you mean by "the satellite's frame". In the first transform the orbits are circular and in the second they are elliptical.

This is why you cannot just automatically say that they are elliptical, you need to actually write down the transform and check. The observations will be the same in either case, but depending on the details of your transform the same observations will result from different shapes.

 

[Janus]

You seem to have mistakenly thought that I was discussing an A series satellite looking at B series satellite, but I was discussing an A series satellite looking at an A series satellite, as I thought I made clear in the post you were quoting from. At that point I was thinking that the orbits of the A series satellites would appear elliptical as it seems Janus also thought in post #55.

My image is for what the spaceship, in an inertial frame and traveling at the same velocity as an A series satellite, would determine what the relative positions of the A series satellites as having, not what an A series satellite would determine.

 

[name123]

The satellites in the same chain always look to be in the same place as seen by one of their number, but this comes under what I said in #88 - you can work out what a camera sees. You still cannot back out from that to get "where they really are now" because "where they really are now" depends on what you mean by "now".

Ok, so by pictures or film footage they always look the same. So if the sphere did have markings, and you knew the size of the sphere and the size of the satellites and the altitude the satellites were orbiting at according to an observer in the centre of the sphere: Is it being said that this information would not be enough for an observer on one of the satellites to calculate the doppler effect, and thus not to account for that in the observations? Or is it perhaps that it would be possible to even accounting for the doppler effect but that would not provide the information as to where they "really" are in relation to you the observer?

 

[name123]

My image is for what the spaceship, in an inertial frame and traveling at the same velocity as an A series satellite, would determine what the relative positions of the A series satellites as having, not what an A series satellite would determine.

I apologise. I had assumed you were considering them to have been the same at the point the A series satellite was in the same frame of reference as the passing spaceship. I was assuming it would have been in the same frame of reference at that point of time (even if not for any period of time). The point of time that its velocity was equal to the passing spaceships and in the same direction. Was I mistaken?

Actually from you answer in post #93, I can tell that I was. What I am not clear on is why when it is in the same rest frame it comes to a different conclusion from the spaceship in the same rest frame, regarding the other satellite positions at that point.

 

[jbriggs444]

in relation to you the observer?

An observer does not uniquely define a reference frame. For flat space-time and inertial observers, there is an obvious way to define an associated reference frame. But there observers do not qualify.

at the point the A series satellite was in the same frame of reference as the passing spaceship.

Huh? Frames of reference are not things that you can be "in".

 

[Ibix]

Ok, so by pictures or film footage they always look the same. So if the sphere did have markings, and you knew the size of the sphere and the size of the satellites and the altitude the satellites were orbiting at according to an observer in the centre of the sphere: Is it being said that this information would not be enough for an observer on one of the satellites to calculate the doppler effect, and thus not to account for that in the observations?

That specifies the ephemerae of the satellites' orbits in the sphere-centred inertial frame. You can use this information to derive the positions of the satellites in that frame, yes. But that is not the rest frame of any satellite; you still haven't specified that, and until you do you cannot say how the satellite interprets things. Unless you're happy for the satellite to use the sphere-centred inertial frame (in which it is moving).

Or is it perhaps that it would be possible to even accounting for the doppler effect but that would not provide the information as to where they "really" are in relation to you the observer?

There are an infinite number of ways of accounting for the Doppler, depending on which choice of coordinates you make. As has been said about forty times now!

 

[name123]

That specifies the ephemerae of the satellites' orbits in the sphere-centred inertial frame. You can use this information to derive the positions of the satellites in that frame, yes. But that is not the rest frame of any satellite; you still haven't specified that, and until you do you cannot say how the satellite interprets things. Unless you're happy for the satellite to use the sphere-centred inertial frame (in which it is moving).
There are an infinite number of ways of accounting for the Doppler, depending on which choice of coordinates you make. As has been said about forty times now!

Well what about the rest frame of a satellite at a given point of time? The positions of the other satellites at that point of time according to the satellite in that rest frame at that point of time.

 

[PeterDonis]

what about the rest frame of a satellite at a given point of time? The positions of the other satellites at that point of time according to the satellite in that rest frame at that point of time.

That's what @Janus has been describing for you. But the satellite is only at rest in this frame for that instant of time, so it doesn't work as "the satellite's perspective" globally.

 

[name123]

Huh? Frames of reference are not things that you can be "in".

My fault. What I meant was when it was at rest with respect to the spaceship. I was not clear why at that point they would come to a different conclusion about the positions and clock speeds of the other satellites.

 

[name123]

That's what @Janus has been describing for you. But the satellite is only at rest in this frame for that instant of time, so it doesn't work as "the satellite's perspective" globally.

No I realize that, but I am just considering their relative perspectives at that point in time, and curious as to why they would be different.

 

[Ibix]

My fault. What I meant was when it was at rest with respect to the spaceship. I was not clear why at that point they would come to a different conclusion about the positions and clock speeds of the other satellites.

Because clock rates aren't something you can define at an instant in time. Take a photo of two clocks. Can you tell if they both tick at the same rate from that snapshot? No - one could have stopped, even. You need to look at two separate times, and then the ship and the satellite aren't co-moving for at least one of those.

 

[Dale]

Unless you're happy for the satellite to use the sphere-centred inertial frame (in which it is moving).

Which is a perfectly valid choice too. In fact, the GPS system uses essentially this approach.