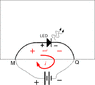Semicircular ring falling through a Magnetic Field

[zorro]

Homework Statement

A thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic field B (see fig). At the position MNQ, speed of the ring is v and the potential difference developed across the ring is - (options are given)

The Attempt at a Solution

First of all, I am not sure whether we can find the flux throug the semi-circle because it does not form a closed loop.

Assuming we can find it out ,
Φ = BπR²/2

The rate of change of magnetic flux is 0 (RHS is constant)
Hence the e.m.f. induced is 0.

The answer doesnot match :|

 

[collinsmark]

First of all, I am not sure whether we can find the flux throug the semi-circle because it does not form a closed loop.

That just means that there won't be a current flowing through the conductor. But there can still be an induced emf.

Assuming we can find it out ,
Φ = BπR²/2

Looks okay to me so far, for the instant that the semicircular ring is at position position MNQ

The rate of change of magnetic flux is 0 (RHS is constant)
Hence the e.m.f. induced is 0.

Don't jump to conclusions! I agree that the rate of change of the magnetic field is zero, but is that also true for the flux?

By definition,

Φ = BA​

and

ε = -dΦ/dt​

thus,

ε = -d(BA)/dt.​

We know that B is a constant, but what about the area A? At the moment the semicircular loop passes through position MNQ and after, does the area defined by the section of the hoop that happens to be within the magnetic field change with time?

 

[zorro]

We know that B is a constant, but what about the area A? At the moment the semicircular loop passes through position MNQ and after, does the area defined by the section of the hoop that happens to be within the magnetic field change with time?

Just before the semi-ring reaches the position MNQ, there is no change in the area it encloses. So there should not be any E.M.F.
E.M.F is induced only after it starts passing through this position.

 

[Dadface]

Hello Abdul,E=-BdA/dt but B is constant so you are trying to find dA/dt which is the area swept out in one second.Try extending your sketch as follows:
1. Draw the semicircle as you did above.
2. Draw the semicircle again but after it has moved to a lower position.
3. Shade in the area swept out by the semicircle.

From this you should be able to see what the area would be for one second and a velocity v.
(assume that the semicircle remains in the field,the situation is different as it enters and emerges)

 

[zorro]

Hello Abdul,E=-BdA/dt but B is constant so you are trying to find dA/dt which is the area swept out in one second.Try extending your sketch as follows:
1. Draw the semicircle as you did above.
2. Draw the semicircle again but after it has moved to a lower position.
3. Shade in the area swept out by the semicircle.

From this you should be able to see what the area would be for one second and a velocity v.
(assume that the semicircle remains in the field,the situation is different as it enters and emerges)

See the attached figure.
What do I deduce from the area swept? I think finding out that area as a function of time is tedious.

 

[Dadface]

Abdul,I think it is only the horizontal elements of the wire that cut the field.The problem is equivelent to a straight wire of length equal to 2r moving with velocity v.Look at your diagram and draw two diameters one for the wire in the top position and two for the wire in the bottom position.From this can you see a non tedious way of finding the area?

 

[zorro]

Do you mean that area swept by the diameter equals the area swept by the ring in a fixed time?

 

[Dadface]

Have a look.Subtract the area above the top diameter and add this to the area above the bottom diameter.How,if at all,does the area swept out by the diameter differ from the area you shaded?

 

[zorro]

Oh yes - the areas swept are same.
So the induced EMF is E=2BRv
Last question - which point is at a higher potential - M or Q?

 

[collinsmark]

Oh yes - the areas swept are same.
So the induced EMF is E=2BRv

'Looks good to me. That's what I got for the situation where the entire semicircular piece of wire is in the field.

Last question - which point is at a higher potential - M or Q?

Recall,

F = qv x B.​

Now imagine that wire contains some positive charges on it (which it actually does. It also contains an equal amount of negative charges too, but let's just consider the positive charges for the moment).

Using the right-hand-rule (or whatever applicable rule you wish to use for the cross product), which direction would these positive charges be "pushed"?

Now, hypothetically, if you were to take the wire out of the magnetic field and attach it to the terminals of a battery, what polarity would use such that the current flows in the same direction as those positive charges were previously "pushed"?

(Now if you were curious and wanted to consider the negative charges too, they will be forced in the opposite direction that the positive charges were, in the situation where the wire is moving in the magnetic field. And when taken out of the field and connected to the battery, the "current" flows in the opposite direction as the negative charges, so the answer still comes out to be the same as before.)

 

[zorro]

The positive charges will be pushed towards right. So Q is at a higher potential.
Thanks alot!

 

[collinsmark]

The positive charges will be pushed towards right. So Q is at a higher potential.
Thanks alot!

Wait, hold on.

I agree that the positive charges would be pushed toward the right. .

But if you took the wire out of the magnetic field, attached it to a battery such that the battery's positive terminal was on Q and the negative terminal on M, the current (thus positive charges) would flow through the wire to the left.

So you should re-think that last part.

[Edit: If you'd like to think about it another way, the positive side of the induced emf is going to push the positive charges in the wire away from it. Which side of the wire are the positive charges being pushed away from?]

 

[zorro]

Wait, hold on.

I agree that the positive charges would be pushed toward the right. .

But if you took the wire out of the magnetic field, attached it to a battery such that the battery's positive terminal was on Q and the negative terminal on M, the current (thus positive charges) would flow through the wire to the left.

So you should re-think that last part.

The ring doesnot form a closed loop. So you cannot hypothetically take the wire out of the magnetic field and attach it to a battery as that is applicable only in the case of closed loops .

 

[zorro]

I thought about one more possibility while thinking about the problem.
What will be the e.m.f induced int the semi-ring if the velocity is parallel to the diameter?
Will it be same as above - 2BRv ?

 

[Dadface]

Try it out,use the same method as before.

 

[zorro]

I am confused - in this case the area swept by the diameter is 0 whereas it is not so for the semi-ring.

 

[Dadface]

In the original case there was an area swept out by the horizontal elements of the wire and zero area swept out by the vertical elements the system being equivelent to a horizontal wire of length equal to the diameter.In this new case the area will be swept out by vertical elements of the wire and,as you noticed,zero area swept out by the horizontal elements.Draw a sketch as you did before and you should be able to see it.

 

[zorro]

There are no significant vertical elements - only at the ends on the wire. So I think the area swept by them will be negligible and e.m.f induced is 0. Is it fine?

 

[Dadface]

There are no significant vertical elements - only at the ends on the wire. So I think the area swept by them will be negligible and e.m.f induced is 0. Is it fine?

No,an emf will be induced.Each tiny element of wire can be considered to have a horizontal and a vertical component being vertical only at the two ends and horizontal only in the middle.The effective sum of the horizontal lengths of all the elements=2r,what is the effective sum of the vertical lengths?

 

[zorro]

Is it πR ?

 

[Dadface]

The vertical distance between the two ends and the top of the semicircle(the height)=r.Have another look at your original diagram.

 

[zorro]

ok. Is the emf induced = Brv ?

 

[Dadface]

Yes.

 

[zorro]

I spent last 30 minutes thinking about this problem
After a careful analysis, it seems that I don't agree with your previous answer.

According to me the e.m.f. induced should be 0 in this case. Here is my explanation -
If you consider a quarter of the semi-circle (say left one), then you will find out that the vertical projection of this quarter along y-axis is towards + y-axis (upwards). You can resolve this into a vertical conductor of length r. E.M.F produced is Brv.
Now if you consider the next quarter, its vertical projection is directed along - y axis. E.M.F. produced is - Brv.
So the e.m.f s induced across these two quarters cancel each other. Hence the e.m.f. induced is 0.

If you take a look at the previous question, each quarter has the horizontal projection towards the positive x-axis. So the e.m.f. due to each projection gets added up.

I hope I am correct.

 

[Dadface]

In your question the ring was moving parallel to the diameter,in other words both quarters were moving in the same x direction.Imagine bringing the two ends together so they touched and then straightening the whole thing so that in effect you have a single vertical wire made of two equal length vertical wires in contact.There is no cancelling,the emf across the whole thing being the same in size and direction as the emf across each half when considered separately.Of course the length will now be pi*r.

 

[zorro]

In your analogy, you are actually stretching the semi-ring into a straight wire of length πR and finding the e.m.f. (indirectly though)
But that is not correct as there will be a small bend in between and the direction of movement of charged particles (whether negative or positive) is reversed. Consider the left wire (in your case), the lorentz force on a positively charged particle is upwards. It is again upwards in the right wire. Assume that the positively charged particles form a continuous tube. These two opposing forces cancel each other. So there is no movement of charged particles. Hence e.m.f. induced is 0 again.

 

[Dadface]

In my analogy if the two sides make contact along their length then the whole thing can be considered as a thicker single wire.It is the movement of charged particles(electrons)along the wire/ring that causes a negative charge to build up at one end with a resulting equal positive charge at the other and this is what actually causes the emf to be developed.Equilibrium is reached when the repulsive force per electron due to the charge build up becomes equal to the Lorentz force this being when e=Blv(l being equivelent length of structure)

 

[zorro]

If you consider the semi-ring to be a thick wire, then you are changing the question i.e. you are forming a closed loop ( by merging the open ends into one wire ). You can do something else - keep the wire insulated electrically and bring them close enough. Then apply what I told in my previous post. Refer the figure -

The distance between each wire is very very small. It is magnified for a clear view.

 

[Dadface]

In your previous post you gave the example of the force on positive charges being upwards in both the left and right wire.Well,the force on like charged particles is indeed in the same direction for both wires,or in all sections of a single wire or whatever arrangement is used.It is only some electrons that are free to move and it is because the force is in the same direction for particles of like charge that an emf is induced in the first place so I don't understand your point.Are you saying that there are two forces in the same direction which cancel each other out.Anyway, its 12 ocklock here and time for bed.

 

[zorro]

Well I just modeled it that way to prove your point wrong. I assumed all the positively charged particles to form a continuous incompressible stream. There is a pushing force acting on each end of the vertical wires. If the stream of electrons in the left wire gets pushed upwards, the force in the right wire pushes it upwards to cancel the motion. Refer figure -

You can also consider it this way - the left end of the wire forms a positive terminal of an imaginary battery . Similarly the right end forms a positive terminal resulting in opposition of batteries and cancelling of e.m.f.

There can be some flaws in this explanation. I just modeled it my way.
But I still base my confident explanation in post number 24.

 

[collinsmark]

Wait, hold on.

I agree that the positive charges would be pushed toward the right. .

But if you took the wire out of the magnetic field, attached it to a battery such that the battery's positive terminal was on Q and the negative terminal on M, the current (thus positive charges) would flow through the wire to the left.

So you should re-think that last part.

[Edit: If you'd like to think about it another way, the positive side of the induced emf is going to push the positive charges in the wire away from it. Which side of the wire are the positive charges being pushed away from?]

The ring doesnot form a closed loop. So you cannot hypothetically take the wire out of the magnetic field and attach it to a battery as that is applicable only in the case of closed loops .

You can do anything you want to hypothetically, hypothetically speaking.

What I was attempting to do was illustrate an important point. There is an emf induced on the semicircle, even if it is isn't a closed loop. Just like a battery will have a positive and negative terminals on it, even if it doesn't happen to be connected to anything at a particular time.

It's not valid to state, "a battery, standing by itself, does not have positive or negative terminals because its not conducting current." The truth is that it has an emf across the terminals, and it also has a polarity, whether it is conducing current or not.

And one method to determine the battery's polarity is to determine which direction the current would flow when connected in a closed loop, even if that process is done hypothetically.

Here, the wire is not analogous to the battery itself. But the wire will have an emf induced across it as if a battery was connected to it, even if there is no current. If you had a voltmeter connected to the moving wire, you could measure this induced emf.

I thought about one more possibility while thinking about the problem.
What will be the e.m.f induced int the semi-ring if the velocity is parallel to the diameter?
Will it be same as above - 2BRv ?

You and Dadface have discussed this already to some extent, but I think there is some confusion that I want to clear up.

There is an induced emf across the wire, in this second situation (where the wire moves to the side instead of down). But it's not induced between points M and Q. The potential between points M and Q is zero. But there is an non-zero induced emf between points N and M, which is the same emf induced between points N and Q. And as you have already calculated, the value of the emf is Brv. I just wanted to make sure we're all on the same page there. I'll leave it up to you to determine the polarity of the emf.

 

[zorro]

What I was attempting to do was illustrate an important point. There is an emf induced on the semicircle, even if it is isn't a closed loop. Just like a battery will have a positive and negative terminals on it, even if it doesn't happen to be connected to anything at a particular time.

It's not valid to state, "a battery, standing by itself, does not have positive or negative terminals because its not conducting current." The truth is that it has an emf across the terminals, and it also has a polarity, whether it is conducing current or not.

And one method to determine the battery's polarity is to determine which direction the current would flow when connected in a closed loop, even if that process is done hypothetically.

I agree with you.
What confused me was your statement -

But if you took the wire out of the magnetic field, attached it to a battery such that the battery's positive terminal was on Q and the negative terminal on M, the current (thus positive charges) would flow through the wire to the left.

So you should re-think that last part.

If you don't connect the battery, the positive charges move towards right (the force acting is towards right) and get concentrated there creating a higher potential.

I agree that if a battery is attached with positive terminal on Q and negative terminal on M, the positive charges would flow towards left ( the point Q will be still at higher potential). This method is fine if you just want to find out the polarity. You cannot conclude that the force acting on the positive particles is towards left.

Its towards right.

 

[collinsmark]

If you don't connect the battery, the positive charges move towards right (the force acting is towards right) and get concentrated there creating a higher potential.

I agree that if a battery is attached with positive terminal on Q and negative terminal on M, the positive charges would flow towards left ( the point Q will be still at higher potential). This method is fine if you just want to find out the polarity. You cannot conclude that the force acting on the positive particles is towards left.

Its towards right.

Yes! that's right! We're both in agreement (and always were) that the positive charges are forced to the right. There is no disagreement on that point.

What I was requesting that you rethink is this statement:

The positive charges will be pushed towards right. So Q is at a higher potential.

That's what I disagree with.

The positive charges feel a force toward the right because Q has the lower potential, not higher. The force on the charges is an effect of the emf, not the cause.

I know this can be confusing. But perhaps this link might clear up some of the confusion. Pay careful attention to the polarity of the induced emf, and the corresponding induced current in the figures.
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elevol.html#c2"

 

[zorro]

The positive charges feel a force toward the right because Q has the lower potential, not higher. The force on the charges is an effect of the emf, not the cause.

I know this can be confusing. But perhaps this link might clear up some of the confusion. Pay careful attention to the polarity of the induced emf, and the corresponding induced current in the figures.
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elevol.html#c2"

I completely agree with the matter given in that site.
But the basic difference here is that the wire does not form a closed loop. What you said will be true if the wire forms a closed loop ( I think so ).
Do you have any material that provides an explanation of induced e.m.f. in an open loop?

 

[collinsmark]

I completely agree with the matter given in that site.
But the basic difference here is that the wire does not form a closed loop. What you said will be true if the wire forms a closed loop ( I think so ).
Do you have any material that provides an explanation of induced e.m.f. in an open loop?

Yes, the site I gave you provides about the best explanation available. The first diagram in the linked page shows the polarity of a rod in an open loop.

The piece of knowledge to take home with you at the end of the day is that the induced emf is the same whether the loop is open or closed. It doesn't matter if there is an open or closed loop. The induced emf is independent of that.

 

[Dadface]

Nice link collinsmark.Do you see it now Abdul.Closed loop or open loop,semi circular shape,rectangular shape or any other shape,the theory needed to calculate the emf is the same.There is an initial vertical flow of charge resulting in a charge difference and therefore an emf between the top and bottom of the circuit.

 

[zorro]

The positive charges feel a force toward the right because Q has the lower potential, not higher. The force on the charges is an effect of the emf, not the cause.

What confused me so much was about the difference between induced electric field and electric field due to the movement of charges.
We don't define a potential for an induced electric field. Moreover, an induced electric field is independent of any charge.
The potential we were talking about was due to the electric field created by the movement of charges. Refer the figure.

Both the electric fields are along the same direction. Is Q still not at a higher potential?

 

[hikaru1221]

Hi all,

@Abdul Quadeer: You're self-contradicting.

Moreover, an induced electric field is independent of any charge.

If it's independent of the charge or the flow of charge, then why does it depend on whether the loop is open or closed?

I would like to use the term "developed E-field" instead of "induced E-field", as it is not a real E-field and also not formed by magnetic induction, as observed in the reference frame of the ground: \vec{E}^*=\vec{v}\times\vec{B} .
The developed emf: e = \int_M^Q \vec{E}^*d\vec{l} = \int_M^Q (\vec{v}\times\vec{B} )d\vec{l} , independent of the charge and also the flow of charge.
This is a true emf. We don't care about what kind of force developed inside the emf "source". As long as the electron is propelled and given some amount of energy when moving through this "source", it has emf, by definition.
By the way, electric potential is defined for the external circuit in this case. I'm not sure whether it's valid for the semi-ring or not.

@collinsmask: I think this reasoning of yours is a fallacy:

But if you took the wire out of the magnetic field, attached it to a battery such that the battery's positive terminal was on Q and the negative terminal on M, the current (thus positive charges) would flow through the wire to the left.

The wire (and plus the B-field) is a mechanism which has the emf. It is NOT an external circuit. I think the correct equivalent circuit where we connect a resistor to QM to form a closed loop should be like in my picture. In this case, I think Abdul Quadeer was right.

 

[zorro]

@Abdul Quadeer: You're self-contradicting.

If it's independent of the charge or the flow of charge, then why does it depend on whether the loop is open or closed?

Yes I was wrong.

@collinsmask: I think this reasoning of yours is a fallacy:

The wire (and plus the B-field) is a mechanism which has the emf. It is NOT an external circuit. I think the correct equivalent circuit where we connect a resistor to QM to form a closed loop should be like in my picture. In this case, I think Abdul Quadeer was right.

That was what I meant when I said it doesnot form a closed loop to Collinsmark.

The ring doesnot form a closed loop. So you cannot hypothetically take the wire out of the magnetic field and attach it to a battery as that is applicable only in the case of closed loops .

You can attach a battery only in the case of a closed loop.

 

[collinsmark]

@collinsmask: I think this reasoning of yours is a fallacy:
[...]
The wire (and plus the B-field) is a mechanism which has the emf. It is NOT an external circuit. I think the correct equivalent circuit where we connect a resistor to QM to form a closed loop should be like in my picture. In this case, I think Abdul Quadeer was right.

Hello hikaru1221,

You've got your resistor in the wrong place. We're calculating the induced emf across the moving wire itself. Essentially, the moving wire is the resistor.

For a more concrete example, for illustrative purposes only, let's replace the moving wire/resistor with a polar device, such as an LED. If you want the moving LED to light up it needs to be placed in the correct polarity, and that means M is positive and Q is negative.

That was what I meant when I said it doesnot form a closed loop to Collinsmark.

The ring doesnot form a closed loop. So you cannot hypothetically take the wire out of the magnetic field and attach it to a battery as that is applicable only in the case of closed loops .

You can attach a battery only in the case of a closed loop.

Hello Abdul,

Again all of this is hypothetical to illustrate the point of why M is positive and Q is negative. You can claim that Q is the positive terminal if you wish and you are completely free to do so, but you will dinged on your homework and tests if you are ever asked to specify the polarity. I know this subject can be a little confusing, which is why hypothetical situations and thought experiments are so useful.

So hypothetically, if we removed the magnetic field, and replaced it with a battery, the equivalent circuit is shown below, for the situation where a second wire (outside the magnetic field) is connected between M and Q. (The LED is left in the circuit for illustrative purposes only). The voltage drop goes positive to negative from M to Q. Thus M is the positive terminal, and Q is negative, when considering the moving semicircle of wire itself.

[Edit: Now, if you wish to model the circuit without the second wire (open-loop), such that there is no current, then the above circuit is still the equivalent circuit! It's just that the LED/resistor has infinite resistance. But there is still an efm induced across it the wire. But there is no current because of the infinite resistance (an open loop has infinite resistance, btw), and that's why M is positive and Q is negative when discussing the emf induced across the semicircle of wire itself.]

[Edit: Another reason why some of this can be so confusing is because the correct answer of what the polarity is depends heavily on question of the the polarity of "what".

• If asked "what is the polarity of induced emf across the wire moving in the magnetic field, you should give the answer as I described above. In this case, M is positive and Q is negative. That's because the question is all about the moving wire itself. And the answer must have focus given to the moving wire.
• If instead, the whole system is to be taken as a "black box" that is to function as an electrical generator which has terminals M and Q, and you are asked, "what is the polarity of terminals M and Q on this black box generator?" the answer in this case is that Q is positive and M is negative. That's because the question doesn't involve the moving wire at all per se, and the attention is given to components external to the system.]

 

[hikaru1221]

Hello hikaru1221,

You've got your resistor in the wrong place. We're calculating the induced emf across the moving wire itself. Essentially, the moving wire is the resistor.

The emf is developed on the wire, so the wire is a source itself, regardless of whether its resistance is zero or non-zero. If zero, it's an ideal source; if not, it's simply equivalent to an ideal voltage source in series with a resistor. The resistor I put in the picture was to form AN EXTERNAL CIRCUIT so that THE LOOP IS NOW CLOSED; this resistor is not the internal resistor of the wire. In the lumped model (this is the term that electrical engineers use), the emf is always attributed to a source.

Now let's forget the wire for a while. Say, the wire is some two-ported mechanism where we know for sure a current will go out from terminal Q; we don't care whether it's a source or anything. If we connect an external resistor to Q and M, since the current goes from Q, through this resistor, to M, the potential of Q must be higher than the potential of M, by Ohm's law.

For a more concrete example, for illustrative purposes only, let's replace the moving wire/resistor with a polar device, such as an LED. If you want the moving LED to light up it needs to be placed in the correct polarity, and that means M is positive and Q is negative.

In this example of yours, you already forgot to include a source. If there is no source, there will be no current. The LED alone won't make it equivalent to the emf.
The difference between LED (or any similar device) and the source (the emf) is that while LED is an energy absorption device, the source is generally an energy provision device (except more complicated cases where two or more sources or emf's are involved).

[Edit: Another reason why some of this can be so confusing is because the correct answer of what the polarity is depends heavily on question of the the polarity of "what".

• If asked "what is the polarity of induced emf across the wire moving in the magnetic field, you should give the answer as I described above. In this case, M is positive and Q is negative. That's because the question is all about the moving wire itself. And the answer must have focus given to the moving wire.
• If instead, the whole system is to be taken as a "black box" that is to function as an electrical generator which has terminals M and Q, and you are asked, "what is the polarity of terminals M and Q on this black box generator?" the answer in this case is that Q is positive and M is negative. That's because the question doesn't involve the moving wire at all per se, and the attention is given to components external to the system.]

Abdul Quadeer is asking about the potential - the nature of the field and the phenomenon, not some convention on the polarity (The polarity is just the way people name it after all!). I also have never heard of polarity of emf. Anyway I am not sure if we can even define a potential for such "field" (\vec{E}^*=\vec{v}\times\vec{B} - this "field" only exists inside the wire and is not an independent entity, so I would rather call it "force per unit charge". This term makes even more sense when it comes to emf, as for any voltage source, it is the "force per unit charge" inside the source which develops the emf, regardless of the nature of the force). So I would rather pay attention to the external circuit.

 

[collinsmark]

Abdul Quadeer is asking about the potential - the nature of the field and the phenomenon, not some convention on the polarity (The polarity is just the way people name it after all!).

Looking back to the original inquiry in post #9, I see that you are right. And for that I apologize if I caused a lot of undue confusion.

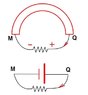
I agree that in the general sense, point Q has the higher potential. By that I mean that a given positive charge q will have higher potential energy at point Q than it would at point M. If I contradicted that in any of my previous posts, I am sorry.

For some reason or another, I had it on my mind that Abdul was asking about the polarity (direction, if you will) of the emf induced on the wire. Maybe it was because I working on two many things at once. I don't remember.

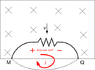
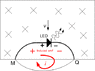
That being said, the induced emf is a voltage and it does have a polarity. If Abdul is ever asked to place this induced emf on a figure showing a moving wire, and label the + and - signs, I want him to get the right answer. And in this case, the '+' sign of the induced emf, on the moving wore itself, corresponds to M and the '-' sign to Q.

This is because, hypothetically, if there is any current due to the induction, it will flow through the moving wire from M to Q. '+' to '-'.

Take a look at the link that I referred to a few posts ago. (I'll link it again here),
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elevol.html#c2"

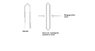
Look at the first figure on the page, where it describes "induced voltage." Notice the polarity of the induced voltage.

Also look at the second and third figures on the page, and take note of the '+' and '-' signs.

This "hyperphysics" page is from the University of Georgia State University. But I don't think they are alone in using this convention in labeling the induced emf in this way. I've seen this sort of thing in other textbooks too.

I think the crux of this seeming contradiction stems from the different questions, "if you are a moving wire, how does the rest of the world seem to you?" and "if you are the rest of the world how does a moving wire seem to you?" It seems this convention of putting the '+' and '-' signs such that the current flows from '+' to '-' though the moving wire is a result of the former question.

 

[hikaru1221]

I agree on the polarity I believe Abdul Quadeer would understand more than he asked for after your post

I think the crux of this seeming contradiction stems from the different questions, "if you are a moving wire, how does the rest of the world seem to you?" and "if you are the rest of the world how does a moving wire seem to you?" It seems this convention of putting the '+' and '-' signs such that the current flows from '+' to '-' though the moving wire is a result of the former question.

I'm no expert at this issue, but since you mentioned this, I would like to point out for Abdul Quadeer that all the reasonings above are in the reference frame of the ground. It would be a different story if we change to the frame of the moving wire.

 

[zorro]

Thank you collinsmark and hikaru1221 for enlightening me with your thoughts.
I got it all now. As hikaru1221 said - I understood more than what I asked.