drMS said:
Hi- It is not clear to me what you mean for long/short arm.
Sorry, I realize I wasn't clear. Thankfully, Jerich made sense of it:
jerich1000 said:
Yes, the first spring mounted to the ground joint will feel the moment created by the very end force at the tail end of the system.
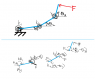
drMS said:
Hi-
take a look to the file mathematica... It was a nice excercise..
Wow this was really amazing. I see how differently you set up the equations. I was thinking of doing something like
Tspring = Tforce
Tspring = [k1+k2 -k2 0 0; -k2 k2+k3 -k3 0; 0 -k3 k3+k4 -k4; 0 0 -k4 k4] x [theta1dot theta2dot theta3dot]'
Tforce = moment on each link = [M1 M2 M3];
where each thetadot is the difference in absolute angles (global angles i.e. to the horizontal).
In this way,
M1 = -Fx*l1*sin(theta1) + Fy*l1*cos(theta1)
M2 = -Fx*l2*sin(theta2) + Fy*l2*cos(theta2)
M3 = ...
I checked this against your formulation drMs and I'm getting the same results so that works!
I was also wondering if you had to do the reverse. Say you knew what the old angles were and you knew what the new angles were and you wanted to determine the Force that was applied. It seems to me that for a mechanism with n+ links, you would only need T2 and T3 equations to simultaneously solve for Fx and Fy. But this is assuming the force is acting on the tip of the last link.
But what if F could be applied anywhere along the mechanism? Is there some way to generalize it so that you could determine both the force and location (which link)?
In my formulation any joint above the joint with the force on it experiences zero M. So I just take the last non zero M, because that's where the force should be being applied to. I can then use another non zero M before that to simultaneously solve F, and then determine the lever arm from the last non zero M equation.
Of course if the force was applied to the first link then you'd have the Force x lever arm = M ambiguity.