Shape of a pinned canvas w/ Lagrange Multipliers

[DuckAmuck]

I'm basically trying to understand the 2-D case of the catenary cable problem. The 1-D case is pretty straightforward, you have a functional of the shape of a cable with a constraint for length and gravity, and you get the explicit function of the shape of a cable.
But if you imagine a square canvas pinned in 4 places:

It is not as obvious what the shape is. I'd expect the result to be a product of two catenary shapes, something like: Sheet(x,y) = Cat(x)*Cat(y). I apply a constraint to surface area of the sheet, but get wacky results. Any help will be appreciated. Thanks.

 

[m3tro]

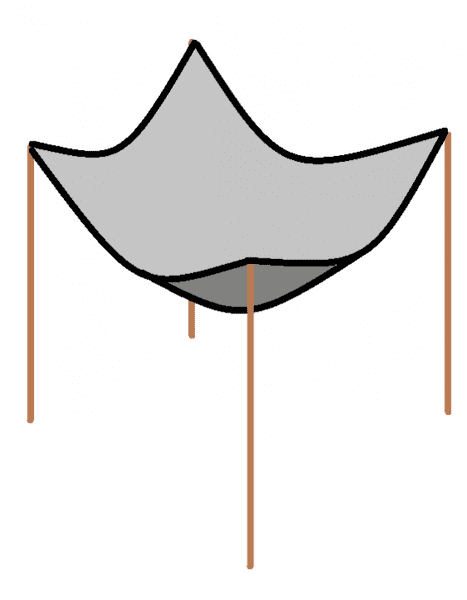
Hey there. The generalization of the catenary problem to 2d is quite complicated.
In the 1-dimensional case, these two questions have the same answer:
1) What is the shape of a line with fixed length L, pinned to points P1 and P2, that has minimal gravitational energy?
2) If I hang a thin rope of length L between points P1 and P2, what shape will it have?
The catenary is the answer to both questions.

But in the 2-dimensional case, these two questions have a different answer:
1) What is the shape of a surface with fixed area A, pinned to points P1, P2, P3, and P4, that has minimal gravitational energy?
2) If I hang a piece of cloth of area A between points P1, P2, P3 and P4, what shape will it have?
These two have a different answer. The problem is that cloths can only deform in an isometric way, that is, in a way that preserves distance along the surface of the cloth. If you cut a piece of blanket into a circle of area A, and if you cut a piece of the top of a parachute into a circle of area A, these two are not equivalent. You will try to flatten the piece of parachute to match the piece of blanket, but wrinkles will appear everywhere when you try to do that. For this same reason, it will be impossible to deform a square blanket into the optimal gravitational shape given by the answer to Question 1.

Question 1 can be easily posed as an optimization problem, as done e.g. here (although note that instead of pinning the surface at 4 points, they require that the surface is pinned along a closed one-dimensional wire frame, which is a more natural generalization of the catenary boundary conditions). Once you find out what is the ideal mathematical surface given your constraints, you would have to weave a cloth specifically in this shape. It will definitely not be useful as a blanket.

Question 2, on the other hand, is much more complicated and has to be solved numerically using triangulated surfaces, see e.g. this, so that the original shape and metric of the blanket can be preserved as it deforms.