Shear force with a mirrored triangular load

[sukibelle]

Homework Statement

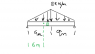
Determine shear force at point D of Beam
http://tinypic.com/r/339m5b6/7

Homework Equations

Sign conventions for cut at d when considering LHSFBD
M = xFy - yFx - cross product...

The Attempt at a Solution

I've found the reaction forces by finding the sum of moments about A (the pin).. Ay and By reaction forces are 9 Kn up..
then i went to find shear force by taking a cut across D and considering the LHS FBD..
I took the moments about A and my answer was really wrong, whereas when I took the sum of the Forces in the Y direction I got the right answer. I want to know why this working out is wrong.. For sum of moments about A.. or why I shouldn't be taking the moments about A?
-2(6)/3*(2*6/9)*(6/2) - 6*(VD) = 0
Here is my FBD for it also
http://tinypic.com/r/2pskdhj/7 (just realized that 3 should be a 9)... The Answer is V = 5 .. i do not get that :(

 

[L2E]

The reason you cannot take the moments about A like you have and determine the shear force diagram is because at the section you cut the beam (D), there is a bending moment equal to some value (46Nm courtesy of http://learntoengineer.com/beam?f=0,u1|18,u2&d=0,9!-2/9*x|9,18!-4_2/9*x&m= ) because you haven't accounted for this in your calculations, you will get an incorrect answer.

if you take the the moments around point A to be equal to 0 you get:
0 =46 - 6*V + Fd*4

Fd = 4, so (46-16)/6 = V = 5

so you can in fact get the correct answer by taking the moments about A, you just need to take into account all the moments.

 

[sukibelle]

Thank you so much! I'm such a goose haha