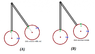
- #1
erisedk
- 374
- 7
Homework Statement
A metal rod of length ‘L’ and mass ‘m’ is pivoted at one end. A thin disc of mass ‘M’ and radius ‘R’ (<L) is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A) The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its centre.
The rod disc system performs SHM in vertical plane after being released from the same displaced position. Which of the following statement(s) is (are) true?
(A) Restoring torque in case A = Restoring torque in case B
(B) restoring torque in case A < Restoring torque in case B
(C) Angular frequency for case A > Angular frequency for case B.
(D) Angular frequency for case A < Angular frequency for case B.
http://studyboard.com/server/uploads/editoruploads/hfbdp6koicft0205ieu8g20uud.png
Homework Equations
##\vec{τ} = I\vec{α}## ... Eqn (i)
##\vec{α} = \dfrac{\vec{a}}{r}## ....Eqn (ii)
##\vec{α} = ω^2θ## ...Eqn (iii)
T for a physical pendulum = ##2π\sqrt{\dfrac{I}{mgd}}## where I is the moment of inertia about the point of suspension and d is the distance of the centre of mass of the rigid body from the point of suspension. (Eqn (iv))
The Attempt at a Solution
To check options C and D,
(case A) I = mL2/3 + ML2
(case B) I = mL2/3 + ML2 + MR2/2
Since I in (case A) is smaller than I in (case B)
According to Eqn (iv) of relevant equations, ωA > ωB (as ω = 2π/T) i.e. (C)
Restoring torque (i.e to check options A and B):
##\vec{α} = ω^2θ##
Since both are displaced from same position θ is the same. So α depends on ω.
Which means αA > αB and IA < IB
Also, I will get canceled out in the torque expression because αI = ω2θI and ω2 is inversely proportional to I.
So, torques will be equal. Hence (A) will hold.
However, the answer is (A) and (D).
Please help?