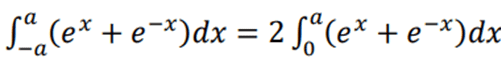SUMMARY
The discussion centers on demonstrating the equality of two integrals involving the functions \( e^x \) and \( e^{-x} \). Participants emphasize the importance of evaluating both integrals to understand the factor of 2 that arises from the symmetry of the function \( f(x) = e^x + e^{-x} \). The equality holds due to the property that if \( f(x) = f(-x) \), then \( \int_{-a}^a f(x) \, dx = 2\int_0^a f(x) \, dx \). This principle is fundamental in calculus and is applicable to similar integrals.
PREREQUISITES
- Understanding of integral calculus, specifically definite integrals.
- Familiarity with the properties of even and odd functions.
- Knowledge of exponential functions, particularly \( e^x \) and \( e^{-x} \).
- Ability to evaluate integrals involving exponential functions.
NEXT STEPS
- Evaluate integrals of the form \( \int_{-a}^a f(x) \, dx \) for various even functions.
- Study the implications of symmetry in integrals, focusing on even and odd functions.
- Learn about the properties of exponential functions and their integrals.
- Explore graphical methods for understanding function behavior, including plotting \( e^x \) and \( e^{-x} \).
USEFUL FOR
Students and educators in calculus, mathematicians exploring integral properties, and anyone seeking to deepen their understanding of symmetry in mathematical functions.