Martin89
- 25
- 1
- Homework Statement
- See below...
- Relevant Equations
- Equations of torque and simple harmonic motion
Hi, I am unsure how to proceed with this problem. I believe that I can correctly calculate the frequency of the oscillations for a bar that is not suspended from a spring but I do not know how to take the effect of the spring into account. The answer given by my professor is $$
f=\frac{1}{2\pi}\sqrt{\frac{3\alpha^2k}{M}}$$
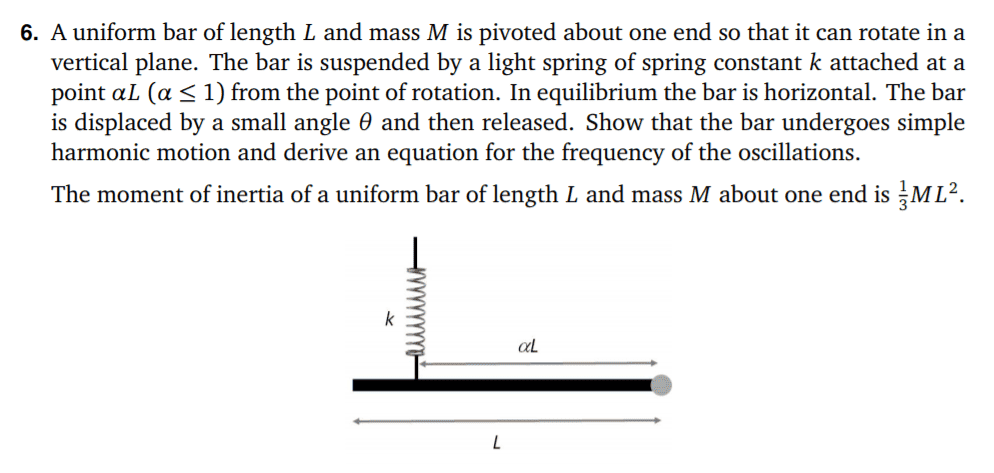
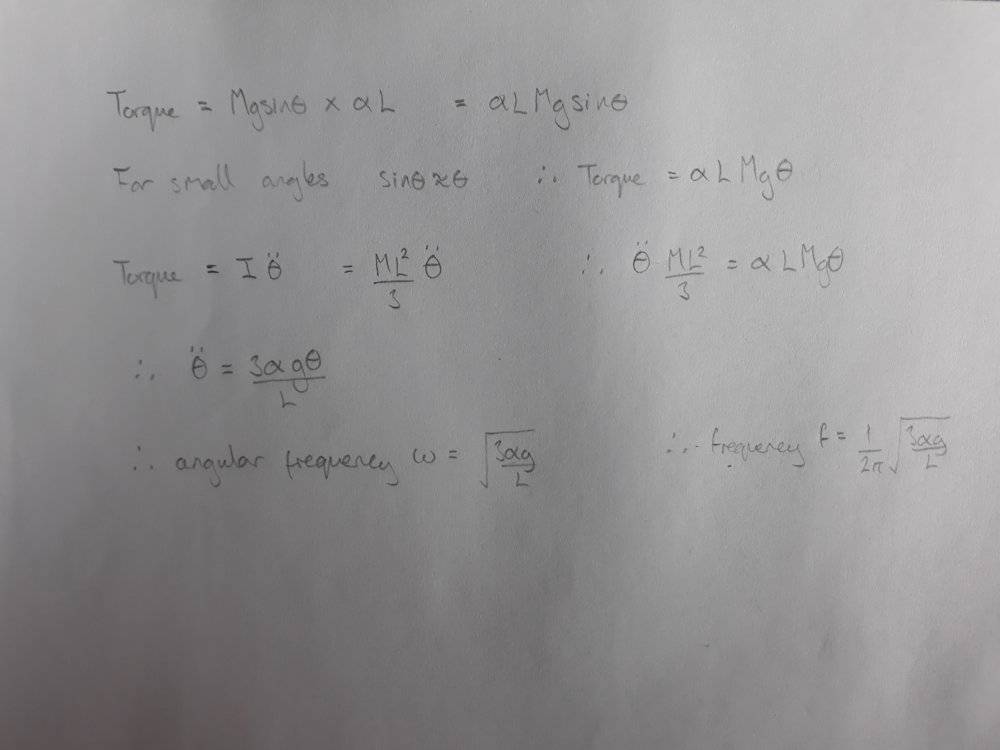
f=\frac{1}{2\pi}\sqrt{\frac{3\alpha^2k}{M}}$$