Ertosthnes
- 49
- 0
Jane wants to swing on a rope across a river. What minimum speed does she need to make it across, and once she's across, what minimum speed does she need to make it back?
Here's what's given:
mass = 47 kg
horizontal wind - call it F - (opposite to her swing) = 120 N
horizontal distance (D) = 50 m
rope length (L) = 40 m
theta = 50 degrees
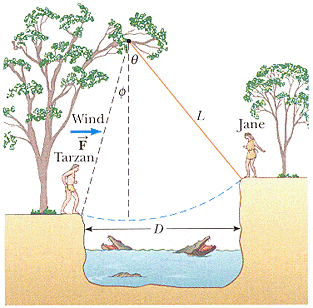
(hopefully you can see the image)
Here's how I started:
D = Lsin(theta) + Lsin(phi)
Plug in the values, and phi = 28.9 degrees
Then, Change in height = Lcos(phi) - Lcos(theta)
Plug in the values, change in height = 9.3 m
From there:
PE(o) + KE(o) + wind = PE(f) + KE(f)
mgh(0) + (1/2)mv(0)^2 - F(w)*D = mgh(f) + (1/2)mv(f)^2
and v(0) = 8.55 m/s
I got that part right. But, now how do I find the minimum velocity to go back? I tried switching the h(0) and h(f) in that last equation to go back, but it didn't work. What's wrong?
Here's what's given:
mass = 47 kg
horizontal wind - call it F - (opposite to her swing) = 120 N
horizontal distance (D) = 50 m
rope length (L) = 40 m
theta = 50 degrees
(hopefully you can see the image)
Here's how I started:
D = Lsin(theta) + Lsin(phi)
Plug in the values, and phi = 28.9 degrees
Then, Change in height = Lcos(phi) - Lcos(theta)
Plug in the values, change in height = 9.3 m
From there:
PE(o) + KE(o) + wind = PE(f) + KE(f)
mgh(0) + (1/2)mv(0)^2 - F(w)*D = mgh(f) + (1/2)mv(f)^2
and v(0) = 8.55 m/s
I got that part right. But, now how do I find the minimum velocity to go back? I tried switching the h(0) and h(f) in that last equation to go back, but it didn't work. What's wrong?