Why Is Path 3 Challenging in This Induction Problem?

[Saffire]

Hiyas, I'm having some problems with this problem, its relatively simple, but I just can't get it right for some odd reason..

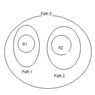
The picture (my awesome paint skills), shows two circular regions R1 and R2 with radii r1 = 22.0 cm and r2= 34.0 cm. In R1 there is a uniform magnetic field B1 = 50 mT into the page and in R2 there is a uniform magnetic field B2 = 75 mT out of the page (ignore any fringing of these fields). Both fields are decreasing at the rate of 7.60 mT/s.

Calculate the integral (E * ds) for each of the three paths.

I've got the first 2, Path 1 and Path 2 by Faraday's law (-A db/dt), but I don't know how to do Path 3.

Any help here would be appreciated. Excuse the poor quality of the picture :)

 

[Chen]

Let V_B be the rate of decrease of the magnetic fields (\frac{dB}{dt}).

For the 3rd path:
\oint E\cdot ds = -\frac{d\phi _B}{dt} = -\frac{{d\phi _B}_1 + {d\phi _B}_2}{dt}

\phi _B_{(t)} = A_{(t)}B_{(t)}
The area is constant, it's only the magnetic field that's changing:
\phi _B_{(t)} = \pi R^2(B_0 - V_Bt)

Since B1 and B2 are in opposite directions, give one of them a minus sign:
{\phi _B}_1 + {\phi _B}_2 = \pi R_1^2(B_0 - V_Bt) - \pi R_2^2(B_0 - V_Bt) = \pi (B_0 - V_Bt)(R_1^2 - R_2^2)
Take the derivative of that:
\frac{{d\phi _B}_1 + {d\phi _B}_2}{dt} = -\pi V_B(R_1^2 - R_2^2)

And therefore:
\oint E\cdot ds = \pi V_B(R_1^2 - R_2^2)

 

[M98Ranger]

Hi there,

I understand that you are having trouble with the third path in this problem. It can be frustrating when something seems simple but you just can't seem to get it right. Let's see if we can work through this together.

First, let's review what we know about Faraday's law and how it applies to this problem. Faraday's law states that the induced electromotive force (EMF) in a closed loop is equal to the negative of the time rate of change of the magnetic flux through the loop. In other words, the EMF is equal to the change in magnetic flux over time.

In this problem, we are given the rate of change of the magnetic field in both regions R1 and R2. We also know the radii of the two regions. Using this information, we can calculate the change in magnetic flux over time for paths 1 and 2.

For path 3, we can use the same approach. We know the radius of the region R3, and we know the rate of change of the magnetic field in that region. So, using Faraday's law, we can calculate the change in magnetic flux over time for path 3 as well.

Once we have the change in magnetic flux over time for all three paths, we can use the formula for EMF (EMF = -dΦ/dt) to calculate the induced EMF for each path. Then, we can use the formula E * ds to calculate the integral for each path.

I hope this helps you understand how to approach the problem for path 3. If you are still having trouble, I would suggest breaking the problem down into smaller steps and making sure you fully understand each step before moving on to the next one. Also, don't hesitate to seek out additional resources or ask for help from a teacher or tutor. With some persistence and practice, I am confident that you will be able to solve this problem successfully. Good luck!