Simple Integrated Circuit Question

In summary, the circuit in question has a maximum voltage of +1.3 V at the drain of Q2 and a minimum voltage of -1.3 V at the drain of Q5. The equation for overdrive voltage of Q4 is VOV4 = VD4 - VS4. Further questions arise about the voltages at the drain and source of Q4 and Q5, with clarification that the drain is always more positive than the source unless the circuit is operated in an inverse mode. The solution manual has a mistake and the correct equation is VOV4 = -1.3 - (-1.5). There is also confusion about the value of R in the circuit, with the correct equation being R = (VS
  • #1
Quincy
228
0
I have a simple conceptual question rather than an actual problem so pardon me for not using the provided template.

There's a question in my Microelectronic Circuits book involving this circuit:

SS figure p7.51.png


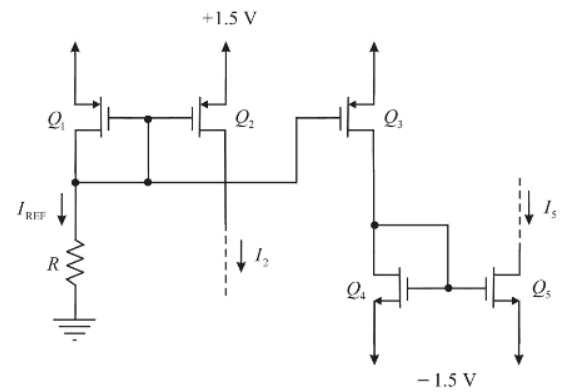
where it states that
voltages at the drain of Q2 can be as high as +1.3 V and voltages at the drain of Q5 can be as low as -1.3 V.

Part of the solution involves this equation:

VOV4 = VD4 - VS4 (equation for overdrive voltage of Q4)

VOV4 = -1.5 - (-1.3)

My question is: Why is VD4 equal to -1.5 V and why is VS4 equal to -1.3 V? -1.3 V is the voltage at the drain of Q5, how did it become the voltage at the source of Q4?
 
Physics news on Phys.org
  • #2
Quincy said:
My question is: Why is VD4 equal to -1.5 V and why is VS4 equal to -1.3 V? -1.3 V is the voltage at the drain of Q5, how did it become the voltage at the source of Q4?
Unfortunately, what you state is incorrect. The drain of D4 will be more positive than the source.
The drain of Q4 is > -1.5V. Perhaps as low as -1.3V but certainly no lower.
The source of Q4 is at -1.5V.
The drain of Q5 can be as low as -1.3V.
For an NMOS. the drain is more positive than the source unless it's operated in the "inverse" mode in which case the labels "drain" and "source" become a matter of semantics. I have never encountered a circuit using the inverse mode, except once which turned out to be a design error. So forget the inverse mode.
 
  • #3
rude man said:
Unfortunately, what you state is incorrect. The drain of D4 will be more positive than the source.
The drain of Q4 is > -1.5V. Perhaps as low as -1.3V but certainly no lower.
The source of Q4 is at -1.5V.
The drain of Q5 can be as low as -1.3V.
For an NMOS. the drain is more positive than the source unless it's operated in the "inverse" mode in which case the labels "drain" and "source" become a matter of semantics. I have never encountered a circuit using the inverse mode, except once which turned out to be a design error. So forget the inverse mode.

Turns out the solution manual had it wrong... it should be VOV4 = -1.3 - (-1.5)
 
  • #4
New question concerning same circuit: Why is R = (VS2 + VGS2)/IREF? Shouldn't it be VD1/IREF?
 
  • #5
Both seem correct.
 
  • #6
Quincy said:
New question concerning same circuit: Why is R = (VS2 + VGS2)/IREF? Shouldn't it be VD1/IREF?

VGS2=VG2-VS2
VS2+VGS2=VG2

VD1=VG2

due to symmetry VD1=VD2
therefore R=(VS2+VGS2)/Iref=VD1/IREF=VD2/IREF
 
  • #7
New question related to same circuit in the initial post: the solution manual states that VDS2max = VOV2 = VGS2 - Vth. My question is why is VDS2max = VOV2? Shouldn't VDS2 = VGS2 since the drain and gate of Q2 are connected?
 
  • #8
Quincy said:
New question related to same circuit in the initial post: the solution manual states that VDS2max = VOV2 = VGS2 - Vth. My question is why is VDS2max = VOV2? Shouldn't VDS2 = VGS2 since the drain and gate of Q2 are connected?
VDS2max is the max allowed D-S voltage. Yes, obviously, VDS2 = VGS2 so therefore you can also say that VOV2 = VGS2max.
 
  • #9
Isn't VOV = VGS - Vth, so shouldn't VOV2 = VGS2max - Vth? (or VOV2 = VDS2max - Vth) rather than VOV2 = VGS2max?
 
  • #10
Quincy said:
Isn't VOV = VGS - Vth, so shouldn't VOV2 = VGS2max - Vth? (or VOV2 = VDS2max - Vth) rather than VOV2 = VGS2max?
VOV in general just means "overvoltage". It could apply to any two transistor terminals.
 
  • #11
rude man said:
VOV in general just means "overvoltage". It could apply to any two transistor terminals.
I get that but what about the threshold voltage (Vth)? The overvoltage is the voltage across two transistor terminals minus the threshold voltage. Why don't we include it in the equation for VOV = VDS2max?
 
  • #12
Quincy said:
I get that but what about the threshold voltage (Vth)? The overvoltage is the voltage across two transistor terminals minus the threshold voltage.
No. The overvoltage is the maximum voltage you can apply between any two terminals. It has nothing to do with Vth or any other transistor parameter.
 
  • #13
rude man said:
No. The overvoltage is the maximum voltage you can apply between any two terminals. It has nothing to do with Vth or any other transistor parameter.

Ah ok. I was confusing it with the overdrive voltage; I thought they were the same thing.
 

Related to Simple Integrated Circuit Question

1. What is a simple integrated circuit?

A simple integrated circuit is a small electronic device that contains multiple electronic components, such as transistors, resistors, and capacitors, all connected together on a single chip. It is commonly used to perform a specific function, such as amplifying or switching signals.

2. How does a simple integrated circuit work?

A simple integrated circuit works by using the properties of the electronic components within it to manipulate and control the flow of electricity. The specific function of the circuit is determined by the way these components are interconnected and how they interact with each other.

3. What are the advantages of using a simple integrated circuit?

The main advantages of using a simple integrated circuit are its small size, low cost, and high reliability. These circuits are also easy to mass produce, making them a popular choice for a wide range of electronic devices.

4. What are some examples of simple integrated circuits?

Some common examples of simple integrated circuits include operational amplifiers, timers, and voltage regulators. These circuits can be found in various electronic devices, such as calculators, radios, and computer components.

5. How are simple integrated circuits designed and manufactured?

Simple integrated circuits are designed using specialized software and are then manufactured using a process called photolithography. This involves creating a pattern on a silicon wafer, which is then etched and layered with different materials to create the circuit components.

Similar threads

How to determine drain-source voltage for this MOSFET amplifier.
    • Engineering and Comp Sci Homework Help
Replies
0
Views
862
Engineering Thevenin Theorem seems to not work in this 1 bit RAM RC circuit
    • Engineering and Comp Sci Homework Help
Replies
2
Views
1K
Engineering Why Does Vout Become Constant in a MOSFET Circuit at High Vin?
    • Engineering and Comp Sci Homework Help
Replies
1
Views
3K
Engineering Basic circuit problem -- Resistor network and a voltage source
    • Engineering and Comp Sci Homework Help
Replies
6
Views
2K
Why Isn't the Drain Voltage in a MOSFET Circuit Equal to 1.8V?
    • Engineering and Comp Sci Homework Help
Replies
4
Views
1K
Engineering Problem regarding a transistor state in a NAND circuit
    • Engineering and Comp Sci Homework Help
Replies
3
Views
2K
How do I calculate the voltage of a diode in a simple electronics circuit?
    • Engineering and Comp Sci Homework Help
Replies
9
Views
1K
MOSFET Transistors as Switches
    • Electrical Engineering
Replies
5
Views
1K
Does Drain Current Increase if Doping Increases?
    • Electrical Engineering
Replies
5
Views
1K
Calculation of current in driven series RLC circuit
    • Introductory Physics Homework Help
Replies
8
Views
423

Hot Threads

Recent Insights

Back
Top