petterik
- 6
- 0
Simple kinetics problem / Dynamics / Simultaneous equations
I've been trying to solve this problem for hours, not finding the solution. Therefore this question to PhysicsForums homeworks section. Question is just part of the problem, but in order to fully understand issue I must have these joint forces to be clear for myself.
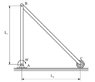
Problem is to solve reaction forces in the joint B when the moment is starting to affect.
Known variables are;
L1 = 0.36 m
L2 = 0.40 m
m1 = 3.2 kg
m2 = 3.2 kg
θ = 26°
M = 30 Nm
roller C is expected to be weightless.
I do have created equations for this. From the F = ma i got all in all six equations. (Described in the attachment.)
I've been trying to solve equations based on the fact that number of equations = Unsolved variables, but finding the needed 3 kinematics equations I am not so sure.
How to find Bx and By with the given data?
EDIT;
- Added picture "equations". - 22.4
- Title corrected.
I've been trying to solve this problem for hours, not finding the solution. Therefore this question to PhysicsForums homeworks section. Question is just part of the problem, but in order to fully understand issue I must have these joint forces to be clear for myself.
Homework Statement
Problem is to solve reaction forces in the joint B when the moment is starting to affect.
Known variables are;
L1 = 0.36 m
L2 = 0.40 m
m1 = 3.2 kg
m2 = 3.2 kg
θ = 26°
M = 30 Nm
roller C is expected to be weightless.
Homework Equations
I do have created equations for this. From the F = ma i got all in all six equations. (Described in the attachment.)
The Attempt at a Solution
I've been trying to solve equations based on the fact that number of equations = Unsolved variables, but finding the needed 3 kinematics equations I am not so sure.
How to find Bx and By with the given data?
EDIT;
- Added picture "equations". - 22.4
- Title corrected.
Attachments
Last edited: