- #1
howsockgothap
- 59
- 0
θθ
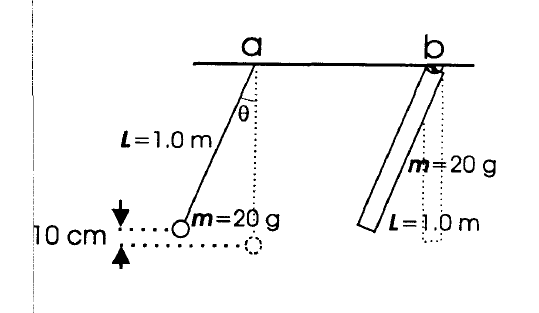
A simple pendulum of mass 20.0 g is suspended by a length of string 1.0 m. It is pulled from equilibrium so that it's raised 10.0 cm and released. Angular position given by θ(t)=θmaxcos(ωt+∅)
What is the period? What is the maximum velocity of the pendulum? What is the phase constant if the mass passes through its lowest point at t=0?
θ(t)=θmaxcos(ωt+∅)
v0=ωA
I found T using gravity and length and am trying to get maximum velocity. My confusion stems mostly from the fact that our professor only discussed acceleration in terms of pendulums and then very briefly.
I thought that I could use v=ωA but I'm a little confused about how I'm supposed to get A for the pendulum, can I just plug in Lsinθ?
For the last part it seems to me I can just use θ=θmaxcos(∅) since t=0, but then I get caught up on what to plug in for θ. It's at its lowest point, so it seems I should simply plug in 0 and am then left with 0=θmaxcos(∅). How do I get θmax? I'm guessing this is tied into my difficulties with part 2.
Homework Statement
A simple pendulum of mass 20.0 g is suspended by a length of string 1.0 m. It is pulled from equilibrium so that it's raised 10.0 cm and released. Angular position given by θ(t)=θmaxcos(ωt+∅)
What is the period? What is the maximum velocity of the pendulum? What is the phase constant if the mass passes through its lowest point at t=0?
Homework Equations
θ(t)=θmaxcos(ωt+∅)
v0=ωA
The Attempt at a Solution
I found T using gravity and length and am trying to get maximum velocity. My confusion stems mostly from the fact that our professor only discussed acceleration in terms of pendulums and then very briefly.
I thought that I could use v=ωA but I'm a little confused about how I'm supposed to get A for the pendulum, can I just plug in Lsinθ?
For the last part it seems to me I can just use θ=θmaxcos(∅) since t=0, but then I get caught up on what to plug in for θ. It's at its lowest point, so it seems I should simply plug in 0 and am then left with 0=θmaxcos(∅). How do I get θmax? I'm guessing this is tied into my difficulties with part 2.