closer
- 18
- 0
A 9.00 kg hanging weight is connected by a string over a light pulley to a 5.00 kg block that is sliding on a flat table (Fig. P5.8). If the coefficient of kinetic friction is 0.560, find the tension in the string.
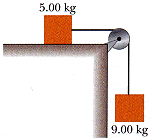
fk = µkN, F = ma, N2 = m2g, 5.00 kg mass = m2, 9.00 kg mass = m1
N = (5)(9.8) = 49
sigma f = ma
T + m2g - fk = (m1 + m2)a
T + (9)(9.8) - (µk)(N) = (14)a
T + (9)(9.8) - (.560)(49) = (14)a
I'm lost at this point. Thanks in advance.
fk = µkN, F = ma, N2 = m2g, 5.00 kg mass = m2, 9.00 kg mass = m1
N = (5)(9.8) = 49
sigma f = ma
T + m2g - fk = (m1 + m2)a
T + (9)(9.8) - (µk)(N) = (14)a
T + (9)(9.8) - (.560)(49) = (14)a
I'm lost at this point. Thanks in advance.
Last edited: