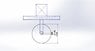
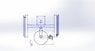
The discussion focuses on calculating the torque required for a flywheel connected to a motor and an eccentric shaft, particularly under a load of 150kg. Participants emphasize the importance of analyzing forces through free body diagrams to determine the worst-case torque scenarios, which may not occur at the dead point but rather when the shaft is in specific positions during its motion. The conversation also highlights that the torque required will vary based on the system's dynamics, including the sinusoidal motion of the platform and the effects of gravity. Recommendations for further reading include engineering texts to better understand the mechanics involved. Ultimately, a thorough force analysis is necessary for accurate motor selection to handle the maximum load.