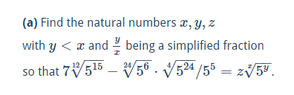MHB Simplification of surds and powers

[danielw]

Hi All

I have this problem. My workings are attached.

View attachment 5870

My answer was:

x=4
y=5
z=6

This is wrong. I don't know where I'm going wrong.

I'd be really grateful if someone could help.

Thanks!

Daniel

View attachment 5869

 

[Darken1]

Can't see the image clearly but I think this is what I would do.
For the multiplication portion
[5^(6/24)][(5^(24/5))/(5^5)]
= [5^(6/24)][(5^(24/5))(5^-5)]

Hint: (x^2)*(x^3) =?
vs (x^2)^3?

 

[Greg]

x=4
y=5
z=6

This is wrong.

No, it's correct! I can't make out your working so I'll post mine for comparison:

$$7\cdot\sqrt[12]{5^{15}}-\sqrt[24]{5^6}\cdot\sqrt[4]{5^{24}}/5^5$$

Rewrite in index notation:

$$=7\cdot5^{5/4}-5^{1/4}\cdot5^6/5^5$$

$$=7\cdot5^{5/4}-5^{1/4+6-5}$$

$$=7\cdot5^{5/4}-5^{5/4}$$

$$=6\cdot5^{5/4}$$

$$=6\sqrt[4]{5^5}$$

You might want to consider learning $\LaTeX$. Quote this post to see the code I have used.