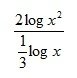Simplifying Expression using Logarithms

[jahaddow]

Simplify the attached expression using any relevant logarithmic rules

I haven't really done much with logarithms, so i didnt know where to start?

 

[rl.bhat]

Simplify the attached expression using any relevant logarithmic rules

I haven't really done much with logarithms, so i didnt know where to start?

Given problem can be written as

log(2)⁴ + log(16)^1/4 + log(1/4)² - log(7/4)

Now use laws of logarithm to simplify.

 

[jahaddow]

the problem is I don't know how to do that?

 

[rl.bhat]

the problem is I don't know how to do that?

log(a) + log(b) = log(ab)

log(a) - log(b) = log(a/b)

 

[HallsofIvy]

Simplify the attached expression using any relevant logarithmic rules

I haven't really done much with logarithms, so i didnt know where to start?

the problem is I don't know how to do that?

Then you should start by learning the "relevant logarithmic rules"!

log(ab)= log(a)+ log(b)

log(a/b)= log(a)- lob(b)

log(a^b)= b log(a)

 

[jahaddow]

Can somebody please demonstrate the question?

 

[Tedjn]

No, you need to solve it yourself; you received sufficient help in the previous posts. Follow that advice.

 

[jahaddow]

That advice dosent get me anywhere!

 

[Tedjn]

Post what you have tried so far pertaining to the advice, or post and ask a question regarding the advice. If I asked you to simplify log(a) + log(b), how would you do it?

 

[jahaddow]

well that would be log(ab)

 

[Tedjn]

Yes, so look at the 3 logarithm rules provided by HallsofIvy and apply them to your problem.

 

[jahaddow]

ok so I'm up to log(2^2) + log(16^1/4) + log(1/4^2) - log(7/4)

 

[Tedjn]

Instead of log(2²) it should be something else. Now, continue until you get an expression with only one log.

 

[jahaddow]

yes ok it would be log(2^4), but then I really am stuck on what to do next!

 

[Tedjn]

well that would be log(ab)

Follow your own advice.

 

[jahaddow]

I don't know how to!

 

[rl.bhat]

I don't know how to!

OK.

What is 2⁴, 16^1/4 and 4²?

Substitute these values in my post #2 and simplify by using the relevant equation given by us.

 

[jahaddow]

Would the answer be log(2/1.75)

 

[jahaddow]

Ok, now I have one which is attached.
I have managed to get to this
logx⁴/logx^1/3
What do I do from here?

 

[jahaddow]

Or would it be 12logx? I don't know.

 

[rl.bhat]

Or would it be 12logx? I don't know.

Your answer for the first problem is correct. But write it as a single number, not in the form of a fraction.

In the second problem from where did you get log(x) along with 12?

 

[jahaddow]

The second problem, I worked out to be just 12 now. But the first problem, 2/1.75 equals a long decimal, so wouldn't I just leave it as a fraction?

 

[rl.bhat]

The second problem, I worked out to be just 12 now. But the first problem, 2/1.75 equals a long decimal, so wouldn't I just leave it as a fraction?

In that case you can write it as 8/7

 

[jahaddow]

Thankyou Very Much! :D

 

[jahaddow]

just one more question, how do I simplify this and express with positive indices.
(18x^3 X 2x^-4)/(4x^-5 X 6x)

 

[rl.bhat]

just one more question, how do I simplify this and express with positive indices.
(18x^3 X 2x^-4)/(4x^-5 X 6x)

\frac{36x^3}{x^4}\times\frac{24x}{x^5}

Now simplify.

 

[xX-Cyanide-Xx]

could someone plese show a bit more detail with the second problem, where did 12 come from.

 

[rl.bhat]

could someone plese show a bit more detail with the second problem, where did 12 come from.

= \frac{4\times3\log{x}}{\log{x}}

Now siplify.

 

[xX-Cyanide-Xx]

I missed the step before that. wheres the 3 come from?

Sorry I am really bad at this.

 

[rl.bhat]

I missed the step before that. wheres the 3 come from?

Sorry I am really bad at this.

\frac{1}{\frac{1}{3}\log{x}} = \frac{3}{\log{x}}

 

[xX-Cyanide-Xx]

Ok i think i got it now. i got it down to 12 by doing this:

2Logx^2 / 1/3Logx
= 4Logx / 1/3Logx
=4 * 3Logx / Logx
=12Logx / Logx
=12

is all the working out correct? if not can u show me the full question with working, all set out as if it were a test?

 

[rl.bhat]

Ok i think i got it now. i got it down to 12 by doing this:

2Logx^2 / 1/3Logx
= 4Logx / 1/3Logx
=4 * 3Logx / Logx
=12Logx / Logx
=12

is all the working out correct? if not can u show me the full question with working, all set out as if it were a test?

Yes. It is correct.

 

[xX-Cyanide-Xx]

cool, but now, back to the first question.

i got up to:
Log(2^4) + Log(16^1/4) + Log(1/4^2)
= Log 16 + Log 4 + Log 0.0625 - Log 1.75
Is this correct?

Then would it go:
Log(16 x 4 x 0.0625) = Log4
= Log(4/1.75)
So y have i got 4/1.75, and jahaddo has 2/1.75??
please help...

 

[xX-Cyanide-Xx]

Can someone please help!
why ismy answer 4/1.75 when jahaddo has 2/1.75??

HELP PLEASE!

 

[rl.bhat]

16^1/4 = 2, not 4.