OmniNewton
- 105
- 5
Mod note: Moved from a homework section
1. Homework Statement
Hello my question more has to do with theory that perhaps deals with algebra.
Why is the following true?
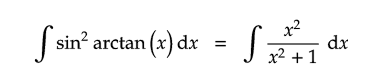
N/A
N/A[/B]
1. Homework Statement
Hello my question more has to do with theory that perhaps deals with algebra.
Why is the following true?
Homework Equations
N/A
The Attempt at a Solution
N/A[/B]
Last edited by a moderator: