- #1
morrobay
Gold Member
- 1,027
- 1,260
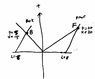
If the below algebra is correct then a light flash originating from the center of a train with .6c will be observed inside both train and platform reference frames as striking the back in less time.
Given : train length= 20ls
v = .6c
lorentz factor .8
As observed from the platform the front train clock=t0 and back train clock = vx/c sq
=t12
As observed from platform clock the light strikes the front of the train at 1/1-.6 (.8)(10)
=20s and strikes the back of the train at 1/1+.6(.8)(10) =5s
this is in accord with (t)front- (t)back= vL/lorentz = .6(20)/.8 =15s
As observed from inside the trains reference frame the light strikes the front at t-vx/LZ
20-.6(12)/.8 =16s
And strikes the back at 5-.6(3)/.8 = 4s
Also both train clocks as observed from platform read t16
So is the above correct. that is from inside both train and platform reference frames the
light strike event at back of train is first ?
morrobay B.S. biology, chemistry minor San Diego State
Given : train length= 20ls
v = .6c
lorentz factor .8
As observed from the platform the front train clock=t0 and back train clock = vx/c sq
=t12
As observed from platform clock the light strikes the front of the train at 1/1-.6 (.8)(10)
=20s and strikes the back of the train at 1/1+.6(.8)(10) =5s
this is in accord with (t)front- (t)back= vL/lorentz = .6(20)/.8 =15s
As observed from inside the trains reference frame the light strikes the front at t-vx/LZ
20-.6(12)/.8 =16s
And strikes the back at 5-.6(3)/.8 = 4s
Also both train clocks as observed from platform read t16
So is the above correct. that is from inside both train and platform reference frames the
light strike event at back of train is first ?
morrobay B.S. biology, chemistry minor San Diego State