Six kinematics problems - all either worked out with wrong answer or conceptual

[clairez93]

Homework Statement

1. Of the following situations, which ones is impossible?
A) a body having velocity east and acceleration east
B) a body having velocity east and acceleration west
C) a body having zero velocity and non-zero acceleration
D) a body having constant acceleration and variable velocity
e) a body having constant velocity and variable acceleration

Answer: E

2. A boy wishes to row across a river in the shortest possible time. He can row at 2 m/s in still water and the river is flowing at 1 m/s. At what angle should he point the bow of his boat? (Picture attached, see #2)

A) 30
B) 45
C) 60
D) 63
E) 90

Answer: E

3. An object, tied to a string, moves in a circle at a constant speed on a horizontal surface, as shown. (see attachment titled #3) The direction of the displacement of this object, as it travels from W to X is:

*see attachment #3*

Answer: E

4. Two projectiles are in flight at the same time. The acceleration of one relative to the other:

A) can be horizontal
B) is always 9.8 m/s^2
C) can be as large as 19.8 m/s^2
D) is zero
E) is none of these

Answer: D

5. A stone is thrown horizontally from the top of a 20-m high hill. It strikes the ground at an angle of 45 degrees. With what speed was it thrown?

A) 14 m/s
B) 20 m/s
C) 28 m/s
D) 32 m/s
E) 40 m/s

Answer: B

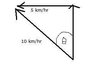
6. A motor boat can travel at 10 km/h in still water. A river flows at 5 km/h west. A boater wishes to cross from the south bank to a point directly opposite on the north bank. At what angle must the boat be headed?

A) 27 degrees E of N
B) 30 degrees E of N
C) 45 degrees E of N
D) 60 degrees E of N
E) depends on width of river

Answer: B

Homework Equations

all kinematics

The Attempt at a Solution

1. For this one, it's a conceptual. My initial thought was C, but then I thought E made sense just as well. The answer the book chose is E, but why does C not work? If there is 0 velocity, then the object is at rest, so there isn't a change in velocity. Therefore there can not be non-zero acceleration. Is there something wrong with this train of thought?

2. See my vector drawing for this problem in the file. I then used arcsin (1/2) to get an angle of 30 degrees. Book says 90. I don't even think 90 degrees makes sense, would it not just push the boat off course and farther away from the destination?

3. I have no idea why this answer would be E, but I'm not sure what a better answer would be, because wouldn't the displacement direction be somewhat diagonal?

4. I have completely no idea what this question is asking for. Do they mean the differences of teh accelerations of the two projectiles? If so, then I suppose I can see that is D, 0.

5. Work:

Let "V" be the final velocity before stone hits surface.

$$V_{fx} = V cos 45$$
$$x = V_{ix}t$$
$$x = \frac{20}{tan(45)} = 20$$
$$y = \frac{1}{2}at^{2}$$
$$20 = \frac{1}{2}(10)t^{2}$$
$$20 = 2V_{ix}$$
$$V_{ix} = 10$$

$$V_{fy} = V sin 45$$
$$V_{ix} = V_{fx} = 10 = V cos 45$$
$$V = \frac{10}{cos 45} = 10\sqrt{2}$$
$$V_{fy} = 10\sqrt{2} sin 45 = 10$$
$$V_{fy}^{2} = V_{fi}^2 + 2ad$$
$$100 = V_{iy}^2 + 2(-10)(20)$$
$$V_{iy} = 10\sqrt{5}$$

$$V_{i} = \sqrt{10^{2} + 10\sqrt{5}^{2}} = 25$$


As you can see, 25 is not an option on this list. Where did I go wrong?

6. see attachment #6 for my vector drawing

I then used arc sin (5/10) to get an angle of 30, however, according to my vector drawing, this angle is west of north, not east of north. Did I draw it wrong?


Much appreciation for any help and looking through my work. :]

 

[queenofbabes]

1) I think choice C is better worded as "constant zero velocity and non-zero acceleration". If you have a non-zero acceleration, obviously velocity cannot be constant, so your train of thought looks correct. Note that it is also possible to have an instantaneous velocity of zero with non-zero acceleration...

2) The question asks for the shortest possible TIME taken to reach the opposite side, it doesn't care how far away on the opposite side you end up. Thus you will want the angle with the largest component pointing towards the opposite bank, which will be 90 degrees.

3) I can't see your attachment yet, but the direction of displacement between 2 points would be the straight line joining them. Displacement is independent of the path taken.

4) What forces (neglecting air resistance) acts on an object in flight? Thus what is the acceleration of said object?

5) You went wrong in your 3rd line, when you said x=20. This doesn't work as it assumes the stone travels in a straight line 45deg to the ground, when in reality it is a parabola.

There is a simple solution to this problem. If the final velocity is at 45deg to the ground, what can you say about its horizontal and vertical components? Thus what is the one thing you need to calculate?

6) I can't see your drawing, but you must have drawn vector for the river current the wrong way. Think about it: if you point your boat west, and the river carrying you further west, where will you end up?

 

[clairez93]

2) Why does the largest component pointing toward the opposite bank allow for the shortest possible time?

3) If you can see the attachment now, the answer choices seemingly make no sense to me. My answer would have been what you said, but it appears that that is not a choice.

4) 9.8 m/s^2, so would that mean that I would subtract the two objects' acceleration to give the ones relative to each other? Or add, I can't remember how to find accelerations relative to other moving objects.

5) The horizontal and vertical would be equal, so I have to calculate the final velocity? I'm not sure how to calculate this though, since all the kinematic formulas seem to have the element of unknown initial velocity.

6) I would think west, thus I my direction chosen would be west of north, however, the answer is east of north.

 

[queenofbabes]

2) The time taken to cross the river would be the width of the river divided by the velocity component in that direction, right? The velocity component parallel to the river doesn't matter here as it doesn't contribute to getting you across the river.

3) Eh, 3 choices are arrows, the 4th is a double arrow (what's that supposed to mean?) and the 5th is a letter "a". Hmmmm?

4) Yes, do just that. What do you get?

5) The question asks for the horizontal velocity, yes? It is unchanged during flight since we ignore air resistance. Since we horizontal and vertical velocities are equal, why don't you just find the vertical velocity? One of the kinematics equations can solve for it immediately!

6) Yes, but you're supposed to go directly opposite, so that's neither east nor west! Thus you have to point EAST to counter the WEST flow of the river!