ksle82
- 30
- 0
https://www.physicsforums.com/attachment.php?attachmentid=6991&stc=1&d=1148442038
rocket1.JPG
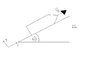
Given the data in the drawing, find the total distance the sled travel.
I got stuck after summing all the forces in the X direction. Help! Here's what i have so far.
Sum of all Forces in X Dir: mgsin(theta) - f = ma
where mgsin(theta) is force due to gravity in the x-dir,
and f is the friction force.
rocket1.JPG
Given the data in the drawing, find the total distance the sled travel.
I got stuck after summing all the forces in the X direction. Help! Here's what i have so far.
Sum of all Forces in X Dir: mgsin(theta) - f = ma
where mgsin(theta) is force due to gravity in the x-dir,
and f is the friction force.