itsalana
- 1
- 0
Restricted Block on Spring
A block of mass m = 2 kg slides back and forth on a frictionless horizontal track. It is attached to a spring with a relaxed length of L = 4 m and a spring constant k = 8 N/m. The spring is initially vertical, which is its the relaxed postion but then the block is pulled d = 4 m to one side.
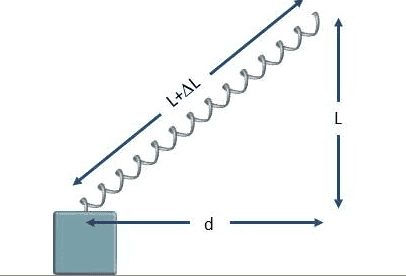
1. By what length is the spring extended?
1.65 M OK
2. What is the potential energy stored in the spring?
10.89 J OK
3. The block is released. What is the maximum speed it attains?
3.3 m/sec OK
I need help with 4 and 5. If someone could just help me, PLEASE?!
4. Let's change the problem a bit. When the spring is vertical (hence, unstretched), the block is given an initial speed equal to 1 times the speed found in part (c). How far from the initial point does the block go along the floor before stopping?
5. What is the magnitude of the acceleration of the block at this point (when the spring is stretched farthest)?
4. So I thought that since on relaxed position, then the only work is on spring
so 1/2 k x^2 with x as 4.
When I got that number, I set that equal to 1/2k (x2-x1).
so I got a -2.72 then I subtracted that to L so 4-2.72. Then i used pythagorean and find d.
It's wrong.
I guess 3.99 and I got it right, but I have no idea how I got 3.99. It was literally a number i just typed in.
5. So for 5, with 3.99 and having no idea how I got 3.99 I don't even know where to start.
Please, if anyone could help me!
I have been working on this question for a total of 4 hours.
Please!
A block of mass m = 2 kg slides back and forth on a frictionless horizontal track. It is attached to a spring with a relaxed length of L = 4 m and a spring constant k = 8 N/m. The spring is initially vertical, which is its the relaxed postion but then the block is pulled d = 4 m to one side.
1. By what length is the spring extended?
1.65 M OK
2. What is the potential energy stored in the spring?
10.89 J OK
3. The block is released. What is the maximum speed it attains?
3.3 m/sec OK
I need help with 4 and 5. If someone could just help me, PLEASE?!
4. Let's change the problem a bit. When the spring is vertical (hence, unstretched), the block is given an initial speed equal to 1 times the speed found in part (c). How far from the initial point does the block go along the floor before stopping?
5. What is the magnitude of the acceleration of the block at this point (when the spring is stretched farthest)?
The Attempt at a Solution
4. So I thought that since on relaxed position, then the only work is on spring
so 1/2 k x^2 with x as 4.
When I got that number, I set that equal to 1/2k (x2-x1).
so I got a -2.72 then I subtracted that to L so 4-2.72. Then i used pythagorean and find d.
It's wrong.
I guess 3.99 and I got it right, but I have no idea how I got 3.99. It was literally a number i just typed in.
5. So for 5, with 3.99 and having no idea how I got 3.99 I don't even know where to start.
Please, if anyone could help me!
I have been working on this question for a total of 4 hours.
Please!
Last edited by a moderator: