aerograce
- 63
- 1
Homework Statement
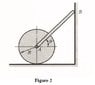
A uniform rod AB of length L and mass m1 is connected by a pin joint to the center of a
uniform disc of radius R and mass m2.
The system is placed in a vertical plane (as shown in Figure 2) and released from rest with
θ=45°.
(a) Draw the free-body diagrams for the rod and the disc.
(b) Find the acceleration of the point B at the instant when the system is released.
You may assume that the pin joint and the vertical wall are frictionless, and the disc rolls
without slipping on the horizontal ground.
Homework Equations
T=Iα;
[a][/B]=[a][/A] + w×(w×[r][/(B/A)]+w'×[r][/(B/A)]
The Attempt at a Solution
My attempt is to first use equilibrium to calculate the static friction force acting on the ground and then through fR=T=Iα to calculate the angular acceleration of point A. This will then help us obtain acceleration of A. Then use the above formula to relate acceleration of B to acceleration of A. But I realize this may be untrue since the system is not in equilibrium initially.