Small ball on top of big ball angle of departure

[guitarphysics]

Homework Statement

My uncle gave me this problem:
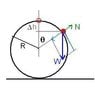
A very small ball of mass m is at the very top of a big ball of radius r and is pushed very lightly (initial velocity is basically zero). What is the angle θ that the small ball's position vector (originating from the origin of the big ball) makes with the vertical y-axis as the small ball comes off of (or departs from) the big ball? PLEASE TELL ME ONLY IF I'M ON THE RIGHT TRACK OR NOT! IF I'M NOT, A HINT WOULD BE GREATLY APPRECIATED (sorry for the all-caps, but I just need a little push in the right direction, not the fully worked out solution).

Homework Equations

ƩF=ma

The Attempt at a Solution

The normal force N exerted on the small ball by the big ball is N=mgcosθ.

ma(y)=mg-Ncosθ
a(y)=g-gcosθcosθ

ma(x)=Nsinθ
a(x)=mgcosθsinθ

a(x) and a(y) being the accelerations of the ball in the x and y coordinates, respectively.

Once I got the accelerations, I was sort of stuck. I'm not really sure what to do next. One thing I've though of is to think of under what conditions the small ball has departed. What I came up with was that when
x>rsinθ,
the small ball has departed. (x being the x position of the small ball). I tried integrating the acceleration in the x direction twice to get position, but that didn't really help.

Does anybody have any hints?

Thanks very much.

 

[ehild]

How do you know that the normal force is mgcosθ?

The small ball moves along a circle till its leaves the surface. What is the net force acting on it if the speed is v?

Friction is not mentioned so energy conservation can be assumed. Can you find the speed v in terms of the angle theta?

The surface of the big ball can only push the small ball away. The small ball leaves the surface if the surface no more exerts force on it, that is, N=0.

ehild

 

[guitarphysics]

Oh, good idea, I'll try finding the energies. Thanks a lot for that tip :).
As for your other points:

I know the normal force is mgcosθ because that's what it would be if the small ball was sliding down a ramp of constant angle θ, and a circle is just basically an infinite number of ramps (of changing angles, of course), so that normal force (mgcosθ) applies to a circle (or infinite ramps) as well, albeit with a changing θ.

I thought about the N=0 thing, but my equations break down for after the small ball has departed.

Thanks for your help!

 

[ehild]

As for your other points:

I know the normal force is mgcosθ because that's what it would be if the small ball was sliding down a ramp of constant angle θ, and a circle is just basically an infinite number of ramps (of changing angles, of course), so that normal force (mgcosθ) applies to a circle (or infinite ramps) as well, albeit with a changing θ.

I thought about the N=0 thing, but my equations break down for after the small ball has departed.

Thanks for your help!

The case is different from moving along a straight line on a flat slope: the ball does not have acceleration component normal to the slope. Moving on the big sphere along its circular path, the small ball has both tangential and normal components of acceleration. The difference between the normal component of gravity and the normal force is equal to the centripetal force: ma_cp. The normal force is not equal to mgcos(θ).

ehild

 

[guitarphysics]

The case is different from moving along a straight line on a flat slope: the ball does not have acceleration component normal to the slope. Moving on the big sphere along its circular path, the small ball has both tangential and normal components of acceleration.

What exactly do you mean by normal components of acceleration?

 

[ehild]

Normal to the surface of the big sphere. The small ball moves along a circle, it must have centripetal acceleration.

ehild

 

[guitarphysics]

Only if it's attracted to the center of the circle (right? I mean, I'm not completely sure, but I don't think there's centripetal acceleration in this case, since it doesn't stay in that path of circular motion).

 

[CWatters]

Only if it's attracted to the center of the circle

Gravity has a component that keeps it attached to the larger ball.

Centripetal force is the component that acts towards the center of the larger ball.

I don't think there's centripetal acceleration in this case, since it doesn't stay in that path of circular motion

While it's on the larger ball it follows a curved path. Centripetal acceleration is allways needed to make anything follow a curved path.

Imagine a car on a roller coaster. How fast can the car go over a hill on the coaster without flying off? If will fail to follow the downward curve of the track if gravity does not provide sufficient centripetal acceleration to make the car follow the same curved path as the track.

Why are you worried about what happens after the small ball comes off? The problem statement is asking how far the small ball travels around the curve of the big ball until the point where it comes off.

 

[guitarphysics]

Aaaaah! I still can't get it...
I tried something else:
a_r is tangenial acceleration, and a_t is tangenial acceleration.

a_t=gsinθ
a_r=v²/r=gcosθ-N/m

N is zero right when the ball is being launched, so

v²/rg=cosθ
arccos v²/rg=θ

Then
U₀-U_f=K₀-K_f
mgh₀-mgh_f=-1/2mv²
2g(h_f-h₀)=v²

U₀ is initial potential energy, U_f is potential energy at the departing point of the small ball, K₀ is initial kinetic energy (0), and K_f is kinetic energy at departure point.
I substitute, and get

arccos[2g(h_f-h₀)/rg]=θ

The problem is, I don't know how to find h_f! (For simplicity, I denote h₀ to be 2r.)

 

[ehild]

hf-ho=Δh. See picture.

ehild

 

[guitarphysics]

hf-ho=Δh. See picture.

ehild

Yes, I'd thought of that, but didn't think it was relevant... Why is it important?

 

[CWatters]

Forget about this problem for a moment.

The centripetal force required to make any object follow a curved path is the familiar equation..

F = MV²/R

This force does not have to be provided by anything connected to the origin of the curve. It just has to act in that direction. For example to make a spacecraft follow a curved path you use a thruster pointing sideways. If you increase the thruster force F the spacecraft turns tighter and R reduces. If you reduce the thruster force F then R will increase. If you turn off the force totally F → ∞ (which is a straight line).

So back to your problem. What provides the force needed for the small ball to follow the curve of the large ball? You had that in your first post...

The normal force N exerted on the small ball by the big ball is N=mgcosθ.

That normal force is caused by the component of gravity acting towards the origin of the curve (the center of the big ball).

So the problem requires you to find the point where the component of force acting towards the center eg mgcos(θ) is not enough to provide the required centripetal force MV²/R. At that point the little ball can no longer follow the tight curve of the big ball R and it starts to follow a path with a larger radius.

or in short when

Mgcos(θ) < MV²/R

Use conservation of energy to find V.

 

[ehild]

Yes, I'd thought of that, but didn't think it was relevant... Why is it important?

You need hf-hi to find the speed at a given theta. hf-hi=-Δh can be expressed in terms of the radius of the circle and theta.


ehild