Solid angles and particle velocities

In summary, the conversation discusses finding the fraction of particles in a gas with velocities in a specific angular range. The speaker is unsure of how to calculate this and draws a diagram to help. Another person mentions a formula for finding the area of a cap on a sphere, but can't remember it. Integration is suggested as a method for finding the formula.
  • #1
quarky2001
34
0
This should be a simple question, but I haven't found a clear explanation anywhere yet.

Suppose that there are a bunch of particles in a gas, with their velocities "uniformly distributed over solid angles", and I want to find out what fraction of particles are traveling with velocities in a certain angular range.

Conceptually, I know what this means. I'm just not sure how to do it - I drew a diagram.

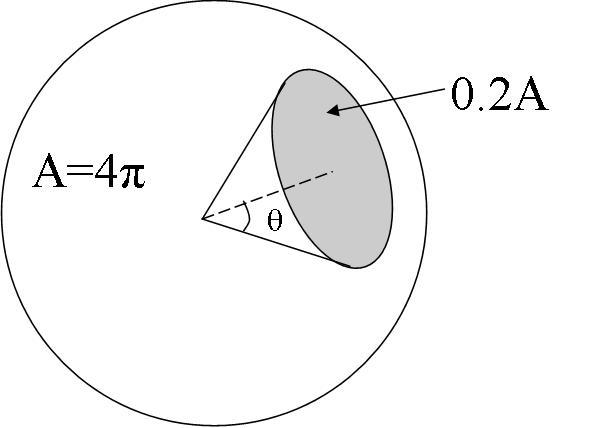
Suppose the shaded area represents 20% of the sphere's total surface area. How do find the angle theta?

attachment.php?attachmentid=31859&stc=1&d=1296657266.jpg
 

Attachments

  • Solidangle.jpg
    Solidangle.jpg
    13.8 KB · Views: 556
Physics news on Phys.org
  • #2
hi quarky2001! :smile:

(have a theta: θ :wink:)

that's called a cap of a sphere of radius θ …

i can't remember the formula for its area :redface:, but it's fairly easy to find by integration :wink:
 

1. What is a solid angle?

A solid angle is a measure of the amount of space an object takes up in three-dimensional space. It is represented in steradians and is analogous to how a regular angle measures the amount of space an object takes up in two-dimensional space.

2. How do you calculate solid angles?

To calculate solid angles, you can use the formula Ω = A/R², where Ω is the solid angle in steradians, A is the area of the surface that the object takes up, and R is the distance from the object to the point where the solid angle is being measured.

3. What is the relationship between solid angles and particle velocities?

Solid angles and particle velocities are related through the concept of flux. Flux is the amount of a physical quantity (such as particles) passing through a given area in a given amount of time. The solid angle determines the size of the area through which the particles are passing, and the velocity determines the rate at which the particles are passing through that area.

4. How are solid angles and particle velocities used in physics?

Solid angles and particle velocities are used in various areas of physics, including electromagnetism and quantum mechanics. In electromagnetism, solid angles are used to calculate electric and magnetic flux, while particle velocities are used to determine the speed and direction of charged particles. In quantum mechanics, solid angles and particle velocities are used to calculate the probability of a particle being in a certain position at a certain time.

5. Can solid angles and particle velocities change?

Yes, solid angles and particle velocities can change depending on the circumstances. For example, if the distance between an object and the point of measurement changes, the solid angle will change accordingly. Similarly, particle velocities can change due to external forces or interactions with other particles.

Similar threads

Finding area of a non right angled triangle
    • Precalculus Mathematics Homework Help
Replies
9
Views
2K
A ball is thrown w/initial speed vi at an angle 𝜃i with the horizontal
    • Introductory Physics Homework Help
Replies
5
Views
294
I How Is Particle Distribution in a Solid Angle Derived in Mechanics?
    • High Energy, Nuclear, Particle Physics
Replies
3
Views
900
Brownian Ratchet (exercise framed by Feynman's Lectures, l. 46)
    • Introductory Physics Homework Help
Replies
32
Views
1K
Magnetic Mirror and particle trap
    • Electromagnetism
Replies
1
Views
681
B Solid angle by placing one disk on a cylinder
    • Other Physics Topics
Replies
1
Views
16K
I I'm calculating more energy out than I put in
    • Classical Physics
2
Replies
61
Views
1K
I Game Design: Set rigid body into a position (Euler angles) using angular velocity
    • General Math
Replies
5
Views
1K
Determine the angular velocity as a function of the angle
    • Introductory Physics Homework Help
2
Replies
39
Views
2K
I Visualizing Solid Angle of a 3d Object (say a Sphere)
    • General Math
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top