AnwaarKhalid
- 8
- 0
Homework Statement
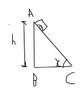
A block of mass m is placed on a triangular block of mass M, which in turn is placed on a horizontal surface as shown. Assume frictionless surfaces. Find the speed of triangular block when the small block reaches the bottom end,
Homework Equations
The Attempt at a Solution
I've uploaded my attempt at a solution. Please, tell me where I did wrong.