Solve by method of Sections/Joints

[seamus258]

Homework Statement

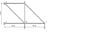
I am having problems trying to solve this truss by both method of sections and joints and require some help which will be much apprecited as i have an exam tomorrow. Thanks in advance.

load at node c is 60kN and 138kN at node d

This is what i have found but not sure if i am right
At node A i have a horizontal reaction <-- 276kN and vertical upward reaction of 207kN.
At node E i have a horizontal reaction --> 276kN.

 

[pongo38]

If your reactions are correct, you can always find out by checking equilibrium using equations as yet not used; for example, taking moments about D should = zero. In this case, I think you may have slipped. Does 207 balance 60 + 138? Try again, or at least check it. Maybe the 60 should be 69? Actually the method of joints is a special case of the method of sections. You cut the structure and replace the cuts with forces that are either known or unknown. Then you make equilibrium statements about each of the objects thus isolated. The diagram you offered is also an example of such an isolated object, and you used the laws of equilibrium to find the reaction components. In this type of question you can check everything with independent equations, and know if you have it right before you leave the examination. That is the best advice I can offer for tomorrow's exam. Best wishes.