odolwa99
- 85
- 0
With this question, I have worked out the correct answers (see the section bordered by BBB), but my original approach was to go by the 1st attempt (bordered by AAA). In the 1st attempt, the h/ k equation results in a single centre, rather than the 2 required to form the 2 separate circle equations. Can anyone help me spot what I need to do to get AAA to work, or is BBB the only approach that will work here?
Many thanks.
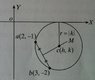
Q. A circle intersects a line at the points a(-3, 0) & b(5, -4). The lines midpoint, m, is (1, -2). The distance from the centre of the circle to m is \sqrt{5}. Find the equations of the 2 circles that satisfy these conditions.
|ab|=\sqrt{(-3-5)^2+(0+4)^2}=\sqrt{80}
1/2 length of chord = \sqrt{20}
|ac|^2=\sqrt{5}^2+\sqrt{20}^2=25\rightarrow |ac|=5 radius
AAA
Slope of |ab|: \frac{-4-0}{5+3}=\frac{-1}{2}
Slope of perpendicular line M = 2
M equation: y+2=2(x-1)\rightarrow 2x-y-4=0
M contains the centre (h, k): 2h-k-4=0
For a 2nd equation containing h & k use (-3, 0):
(h+3)^2+(k-0)^2=k^2\rightarrow h^2+6h+9=0\rightarrow (h+3)(h+3)=0\rightarrow h=-3
For h = -3: 2h-k-4=0\rightarrow k=2(-3)-4\rightarrow k=-10
Thus circle centre is (-3, -10)
AAA
BBB
If radius = 5, then centre of circle containing (-3, 0) = (2, 0)
Equation: (x-2)^2+(y-0)^2=25\rightarrow x^2+y^2-4x-21=0
If radius = 5, then centre of circle containing (5, -4) = (0, -4)
Equation: (x-0)^2+(y+4)^2=25\rightarrow x^2+y^2+8y-9=0
BBB
Many thanks.
Homework Statement
Q. A circle intersects a line at the points a(-3, 0) & b(5, -4). The lines midpoint, m, is (1, -2). The distance from the centre of the circle to m is \sqrt{5}. Find the equations of the 2 circles that satisfy these conditions.
Homework Equations
The Attempt at a Solution
|ab|=\sqrt{(-3-5)^2+(0+4)^2}=\sqrt{80}
1/2 length of chord = \sqrt{20}
|ac|^2=\sqrt{5}^2+\sqrt{20}^2=25\rightarrow |ac|=5 radius
AAA
Slope of |ab|: \frac{-4-0}{5+3}=\frac{-1}{2}
Slope of perpendicular line M = 2
M equation: y+2=2(x-1)\rightarrow 2x-y-4=0
M contains the centre (h, k): 2h-k-4=0
For a 2nd equation containing h & k use (-3, 0):
(h+3)^2+(k-0)^2=k^2\rightarrow h^2+6h+9=0\rightarrow (h+3)(h+3)=0\rightarrow h=-3
For h = -3: 2h-k-4=0\rightarrow k=2(-3)-4\rightarrow k=-10
Thus circle centre is (-3, -10)
AAA
BBB
If radius = 5, then centre of circle containing (-3, 0) = (2, 0)
Equation: (x-2)^2+(y-0)^2=25\rightarrow x^2+y^2-4x-21=0
If radius = 5, then centre of circle containing (5, -4) = (0, -4)
Equation: (x-0)^2+(y+4)^2=25\rightarrow x^2+y^2+8y-9=0
BBB
Last edited: