Solve Equation (1) to Get Equation (2): The Depletion Voltage & Electric Field

[Hayool]

The electric field

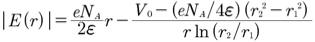...(1)

by saying that

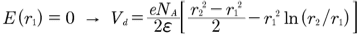...(2)I tried to integrate equation (1) from r2 to r1 but could not get equation(2).

Any suggesting.

Thanks

 

[TSny]

Looks like you should be able to get (2) from (1) with just algebraic manipulation. Did you try letting $E = 0$ in (1) when $r = r_1$and then solving for $V$?

However, I get that (2) should have a positive sign for the last term.

Can you define the symbols $V_d$ and $V_o$ that occur in (1) and (2)?

 

[Hayool]

Looks like you should be able to get (2) from (1) with just algebraic manipulation. Did you try letting $E = 0$ in (1) when $r = r_1$and then solving for $V$?

However, I get that (2) should have a positive sign for the last term.

Can you define the symbols $V_d$ and $V_o$ that occur in (1) and (2)?

Thanks for your prompt respond.

Vo is the difference in potential across the junction
Vd is the depletion voltage
Also for equation (1) the second term has a positive sign.
After doing some algebra i end up with equation (2).

Thanks for the help.