Solve for Net Force on Block C: Homework Problem

[robkom]

Homework Statement

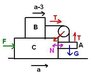
Block C (m = 4 kg) sits on a frictionless horizontal surface. Block B (of m = 2 kg) sits on top of block C, and is attached to a rope that runs over the massless
pulley as shown in the figure. Block A (m = 1 kg) hangs vertically from the rope. With
what horizontal force F must you push Block C so that block A rises with an upward
acceleration of a = 3 m/s²? All surfaces are frictionless.

(a) 12 N
(b) 47 N
(c) 59.8 N \leftarrow This is apparently the correct answer
(d) 15.0 N
(e) None of the above

Figure:
http://www.freeimagehosting.net/t/28bdd.jpg

Homework Equations

Newton's Laws

The Attempt at a Solution

(Viewed as a system)
F = (m_A + m_B + m_C)a
F = (1 kg + 2 kg + 4 kg)a
F = (7 kg)a \leftarrow I must find this acceleration to calculate the force

(From FBD of Block A - choosing UP as the positive direction)
m_Aa_a = T - m_Ag \leftarrow Here, I am using a_a as the 3 m/s² acceleration of the two smaller blocks
T = m_Aa_a + m_Ag
T = (1 kg)(3 m/s²) + (1 kg)(9.8 m/s²)
T = 12.8 N

(From FBD of Block B - choosing RIGHT as the positive direction)
m_B(a - a_a) = T
a = (T + m_Ba_a) / m_B
a = (12.8 N + 6 N) / 2 kg
a = 9.4 m/s²

... Finally, plugging the acceleration into our first equation to find the force:
F = (7 kg)(9.4 m/s²)
F = 65.8 N

If 65.8 is not actually the correct answer, what am I doing wrong in my solution?

Thank you.

 

[ehild]

(Viewed as a system)
F = (m_A + m_B + m_C)a

It is wrong. There are two external forces: F and the weight of A, and the blocks do not move with the same acceleration.

Draw the whole FBD and write out Newton's second law for each block.

ehild

 

[robkom]

Thanks for the quick reply ehild.

Blocks C and A accelerate to the right at the same rate. And blocks A and B accelerate at the same rate. And when viewed as a system, the whole thing accelerates to the right at the same rate. No?

I don't understand how the weight of A is an external force. You mean the force that block A exerts on C (the action-reaction pair of forces)?


I tried it again, keeping in mind what you said, and now I got 47N, which is in the list of possible answers, but is not the correct one.

I drew full FBDs for each block and the system as a whole.

I got 1 equation for each block (for the sum of the forces in the x / horizontal direction) and added them together to get the following:

F_{C on A} + F - F_{A on C} + T = m_Aa + m_Ca + m_Ba_b
F = a(m_A + m_B + m_C) - 3m_B - T

From the FBD of block B:
a_b = T / m_B = 6.4 m/s²
(using 12.8 N for T)

I then used this:
a_b = a - 3 m/s² .. and substituted into the "master equation" at the top to find the force F.

What am I missing?

 

[ehild]

Blocks C and A accelerate to the right at the same rate. And blocks A and B accelerate at the same rate. And when viewed as a system, the whole thing accelerates to the right at the same rate. No?

No. B accelerates with 3 m/s² with respect to C backwards. So its acceleration is a_c-3.

I don't understand how the weight of A is an external force. You mean the force that block
A exerts on C (the action-reaction pair of forces)?

The weight of A is the force the Earth exerts on A. The Earth is not part of the system, so gravity is an external force. The action-reaction pair between A and C is internal force.

I tried it again, keeping in mind what you said, and now I got 47N, which is in the list of possible answers, but is not the correct one.

I drew full FBDs for each block and the system as a whole.

I would like to see your FBD-s. No need to draw an FBD for the system as a whole, as it is the resultant of the separate FBD-s, with only the external forces: F and the weight of C, which determine the motion of the CM of the system.
I show you the forces in the figure. Collect all forces acting on each block. The resultant is equal to the acceleration times mass of that block. Take care on the direction of forces when you write the equations.

ehild

 

[robkom]

Here are my FBDs and equations:

Block A:
http://imageshack.us/photo/my-images/696/q7blocka.jpg/

Block B:
http://imageshack.us/photo/my-images/828/q7blockb.jpg/

Block C:
http://imageshack.us/photo/my-images/200/q7blockc.jpg/

No matter what I do I keep getting 47 N.

Thank you for your help!

 

[ehild]

See my picture: The cord acts also on block C. The chord presses the pulley and the line of the resultant force goes through the axis of the pulley which is fixed to the block. This force has to be taken into account.

The horizontal forces on block C are: F-F_AC-T. Try again, you will get the correct result.
This was a really tricky problem!

ehild