henneh
- 7
- 0
Homework Statement
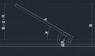
As shown in the attached sketch, derive a non-transcendental equation for the angle, X, given that the parameters A,B, d and R are known variables.
Homework Equations
Basic trig.
The Attempt at a Solution
I have derived an equation which is a function of X as shown below based on simple trignometry:
B = d + R + Rcos(x) + dcos(x) + (A-d-R)sin(x)
Which can be arranged into a (somewhat) easier format:
(R+d)cos(x) + (A-d-R)sin(x) = B - d - R
However I cannot simplify this expression any further. If anyone can help me with this I would really appreciate it! I hope I have been clear in showing the problem geometry, any ambiguities please let me know. Thank you so much.