MrMechanic
- 46
- 0
Homework Statement
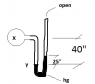
A simple mercury manometer connected into a flow line gives readings as shown in the figure. Local gravity is standard and the mercury density is 0.488lb/in^3. Find the pressure at points X and Y when the flow line and left leg contain (a) air whose density is 0.072lb/ft^3, (b) water whose density is 62.1lb/ft^3. (c) Answer (a) and (b) if the local gravity is g= 30ft/s^2.
ANSWER: (a) 26.90, 26.90, (b) 25.46, 26.90, (c) 26.10 psia
Homework Equations
Pressure = pgh
The Attempt at a Solution
I've done getting Py but I can't find Py at (a)
Also I've tried solving (b) but i can't solve it actually.
Here's my solution on Py at (a)
Py = 14.7psi + (0.072lb/ft^3 / 12^3 in^3)(15) + (0.488lb/in^3)(25) =26.90psi