stinlin
- 72
- 1
Homework Statement
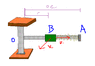
Collar B has a mass of 4 kg and is attached to a spring of constant 1500 N/m and of undeformed length 0.4 m. The system is set in motion with r = 0.2 m, v_theta = 6 m/s, and v_r = 0. Neglecting the mass of the rod and the effect of friction, determine the radial and transverse components of the velocity of the collar when r = 0.5 m.
2. Relevant theories
Conservation of energy - kinetic and potential energy
The Attempt at a Solution
I used conservation of energy :
V_spring_initial = V_spring_final + T_slider_final
x_initial_spring = abs(0.2-0.4)
x_final_spring = abs(0.5-0.4)
I solved for v_r and got 3.35 m/s, which is NOT the right answer.
If I figure out how to solve for v_r, I'm still in the situation where I don't really know how to solve for v_theta. I'm thinking I can determine the force due to the spring and set that equal to m*a_normal, solve for v_theta there (because v^2 = (v_tangential)^2 = (v_theta)^2).
Can I get some help? Thanks a bunch!