Solve simple nonlinear equations in the form [A]x=b

In summary, a nonlinear equation is an equation in which the highest power of the variable is greater than one, resulting in a non-straight line graph. To solve a simple nonlinear equation in the form [A]x=b, one can use algebraic methods like substitution or elimination. Some calculators have the capability to solve nonlinear equations, which is important in fields such as physics, chemistry, and economics. For particularly difficult nonlinear equations, there are special techniques like iteration methods, graphing, or using a computer program. It is important to choose the best method for the specific equation being solved.
  • #1
matthewjames812
1
0
Hi! I have a simple set of nonlinear equations

1) 3x = 30

2) x+2y = 20

3) x + y*z = 15

Clearly the solution to this is (10,5,1) but I want to find a robust way to solve this type of problem [A]x=b (where [A] is a simple function of x) which doesn't involve numerically solving using Newtons method.

n2Hyz.jpg
 

Attachments

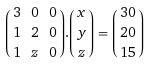
  • n2Hyz.jpg
    n2Hyz.jpg
    2.6 KB · Views: 224
Physics news on Phys.org
  • #2
But it is very trivial to solve these particular examples exactly.
 

1. How do I solve a simple nonlinear equation in the form [A]x=b?

To solve a simple nonlinear equation in the form [A]x=b, you can use various techniques such as substitution, elimination, graphing, or matrix methods. First, identify the type of equation (quadratic, exponential, logarithmic, etc.) and then choose the appropriate method to solve it.

2. What is the difference between a linear and nonlinear equation?

A linear equation is a mathematical expression that can be written in the form of y=mx+b, where m is the slope and b is the y-intercept. Nonlinear equations, on the other hand, cannot be written in this form and may involve exponents, logarithms, or other nonlinear functions.

3. Can I use the same method to solve all types of nonlinear equations?

No, different types of nonlinear equations require different methods for solving. For example, you can use substitution to solve quadratic equations, but you need to use logarithms or graphing to solve exponential equations.

4. How do I know if my solution is correct?

To check if your solution for a nonlinear equation is correct, you can substitute the value of x into the original equation and see if it satisfies the equation. You can also check your answer using a graphing calculator or by solving the equation using a different method.

5. Are there any special cases to consider when solving nonlinear equations?

Yes, there are a few special cases to consider when solving nonlinear equations. For example, some equations may have no real solutions, while others may have multiple solutions. Also, be aware of any restrictions on the domain of the equation, such as when dealing with logarithmic or radical functions.

Similar threads

I Nonlinear least squares vs OLS
    • Set Theory, Logic, Probability, Statistics
Replies
7
Views
474
Finding the center of mass of a simple 2D shape
    • Introductory Physics Homework Help
Replies
9
Views
1K
Time period of SHM & Energy conservation in pulley-spring-block system
    • Introductory Physics Homework Help
Replies
24
Views
1K
A particle moving in a parabolic path in the ##x-y## plane
    • Introductory Physics Homework Help
2
Replies
40
Views
887
I Solving a System of Nonlinear Equations Symbolically
    • General Math
Replies
9
Views
1K
Using Matlab ode45 to solve a simple 2 body problem
    • Introductory Physics Homework Help
Replies
5
Views
3K
Acceleration and Displacement from a Velocity vs. Time Graph
    • Introductory Physics Homework Help
Replies
15
Views
2K
The Relationship Between Masses and Angles in a Pulley System
    • Introductory Physics Homework Help
Replies
29
Views
913
A Nonlinear Wave Equation (Nonlinear Helmholtz)
    • Differential Equations
Replies
1
Views
1K
Solving the operating point of a transformer with a nonlinear B-H curve
    • Electrical Engineering
Replies
4
Views
998

Hot Threads

Recent Insights

Back
Top